Aproksymacja, interpolacja, a może ekstrapolacja? Czy zdarzyło Ci się używać tych pojęć zamiennie? Co one tak naprawdę oznaczają? Jak w MATLABie wykonać aproksymacje, a jak interpolacje? W tym artykule postaram się wytłumaczyć różnice pomiędzy powyższymi metodami oraz pokażę jak użyć MATLABa by zrealizować je poprawnie.
Najczęściej mamy do czynienia z sytuacją, w której wykonujemy eksperyment pomiarowy, zapisujemy wyniki, a następnie przeprowadzamy ich analizę. Dane, niezależnie od tego czy są to przebiegi czasowe czy charakterystyki statyczne, mają postać skończonego zbioru liczb. Przykładem może być charakterystyka temperaturowa dynamicznej wagi pojazdów, w której dokładność ważenia, charakteryzowana przez błąd względny (oś Y) zmienia się wraz ze zmianą temperatury (oś X):
Powyższa charakterystyka niesie informację jakościową. Możemy zaobserwować ogólny trend zmian dokładności pomiaru ze zmianami temperatury. Analiza ilościowa jest tu jednak utrudniona ze względu na rozrzut wyników pomiarowych – nie układają się one idealnie wzdłuż krzywej. Przez to, nie jesteśmy w stanie dokładnie powiedzieć o ile zmieni się dokładność systemu jeżeli temperatura wzrośnie od 0 do 18,5 stopni Celsiusa, nie możemy dokładnie odczytać wartości błędu pomiędzy dwoma punktami pomiarowymi jak również trudno wnioskować o kształcie charakterystyki dla wartości powyżej 55 stopni. Ilościowy opis zmierzonej charakterystyki wymaga zbudowania matematycznego modelu relacji pomiędzy dokładnością ważenia, a temperaturą. Budowa takiego modelu składa się z dwóch etapów:
- przyjęcia klasy modelu – a więc ogólnego wyrażenia matematycznego opisującego dane zjawisko lub obiekt, np.: wielomian 2-go stopnia p1*x^2 + p2*x + p3. Klasę modelu wybiera inżynier na podstawie obserwacji kształtu charakterystyki, przesłanek teoretycznych, ogólnie wiedzy a’priori.
- obliczenia współczynników modelu – czyli konkretnych wartości liczbowych, np. p1 = 1.23, p2 = 0.32, p3 = 0.02. Wartości te są obliczane przez algorytm identyfikacji, zazwyczaj w procesie iteracyjnego poszukiwania minimum funkcji celu. Często stosowaną postacią tej funkcji jest kryterium kwadratowe.
Aproksymacja (curve fitting)
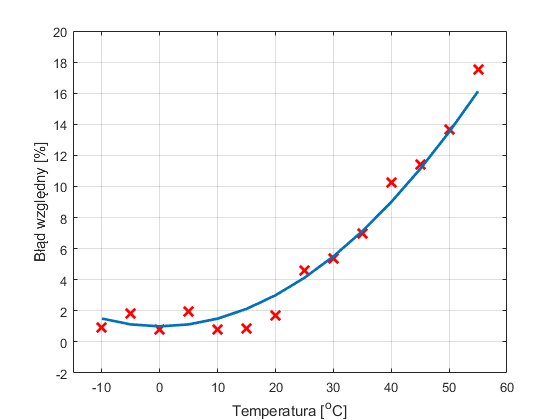
Aproksymacja polega na dopasowaniu krzywej do punktów pomiarowych, przy czym krzywa nie przechodzi dokładnie przez te punkty, lecz odzwierciedla ogólny trend w danych. Celem jest więc znalezienie modelu matematycznego, który będzie reprezentatywny dla badanego zbioru danych. Na rysunku przedstawiono krzywą aproksymującą dane pomiarowe, dla modelu w postaci wielomianu 2 stopnia.
Widać wyraźnie, że krzywa nie przechodzi przez punkty pomiarowe. Dopasowany model odzwierciedla ogólną relacje pomiędzy zmierzonymi wielkościami. Aproksymacje stosujemy więc tam, gdzie zależy nam na matematycznym opisie trendu, a dane pomiarowe charakteryzuje rozrzut wynikający np. z losowego charakteru wykonanego pomiaru. W takiej sytuacji poszukiwanie krzywej przechodzącej przez każdy punkt pomiarowy byłoby niepoprawne i mogłoby prowadzić do błędnych wniosków prowadzonej analizy. Model używany do aproksymacji danych pomiarowych może mieć różną postać, najczęściej jednak stosuje się wielomiany niskiego stopnia.
MATLAB ma wbudowane funkcje służące do aproksymacji danych. Przykładem jest funkcja fit. Jej podstawowa składnia to:
fitobject = fit(x,y,fitType) % dla krzywych fitobject = fit([x,y],z,fitType) % dla powierzchni
gdzie:
- x, y, z – to dane do których zostanie dopasowany model,
- fitType – to rodzaj dopasowywanego modelu,
- fitobject – to obiekt typu cfit dla krzywych i sfit dla powierzchni, zawierający informacje o dopasowanym modelu i jego współczynnikach.
Użycie tej funkcji najlepiej prześledzić na przykładzie, do którego dane pomiarowe znajdziecie tutaj. Za klasę modelu przyjęto wielomian 2-go stopnia (argument ‘poly2’ funkcji fit). Funkcja, zwraca obliczone przez algorytm identyfikacji wartości współczynników dla przyjętej klasy modelu. Zostały one zapisane do zmiennej dModel.
clear all; close all; clc
load dane01 % wczytujemy dane pomiarowe z pliku
% Rysujemy punkty pomiarowe
figure; plot(T, d, 'xr', 'MarkerSize',10)
axis([-15 60 -2 20]);
xlabel('Temperatura [^oC]'); ylabel('Błąd względny [%]');
grid on
% Aproksymacja wielomianem 2-go stopnia (poly2)
dModel = fit(T, d, 'poly2');
dFit = dModel(T);
hold on; plot(T,dFit,'LineWidth',2)
Głównym efektem wykonania programu jest powyższy rysunek oraz model dModel, w postaci wielomianu 2-go stopnia, który został dopasowany do danych pomiarowych T (temperatura), d (błąd względny systemu). Jego postać (klasa modelu), oraz wartości współczynników wynoszą:
dModel =
Linear model Poly2:
dModel(x) = p1*x^2 + p2*x + p3
Coefficients (with 95% confidence bounds):
p1 = 0.004883 (0.003106, 0.006661)
p2 = 0.01033 (-0.07574, 0.09639)
p3 = 0.9881 (0.01144, 1.965)
Interpolacja (Interpolation)
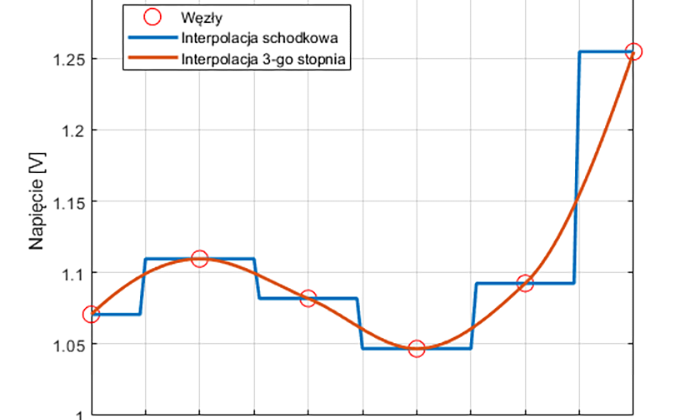
Interpolacja jest metodą numeryczną zbliżoną do aproksymacji z tą różnicą, że dopasowana do danych krzywa przechodzi dokładnie przez punkty pomiarowe. Innymi słowy interpolacja polega na dopasowaniu funkcji do danych w taki sposób, że funkcja ta przyjmuje konkretne wartości w punktach nazywanych węzłami. Na rysunku przedstawiono idee interpolacji.
Widać wyraźnie, że model został dopasowany tak, że reprezentująca go krzywa przechodzi przez punkty pomiarowe. Podstawy matematyczne interpolacji wykraczają daleko poza treść tego artykułu. Warto jednak pamiętać o prostej zasadzie: dla n punktów pomiarowych można dopasować wielomian rzędu n-1. I tak, dla dwóch punktów możemy dopasować model pierwszego rzędu, czyli prostą. Dla trzech punktów, możemy dopasować wielomian 2-go rzędu. I tak dalej. Interpolacja jest często używana, do obliczania wartości funkcji pomiędzy węzłami. Podobnie jak w przypadku aproksymacji, również interpolacja jest zaimplementowana we wbudowanej funkcji MATLABa.
vq = interp1(x,v,xq,method)
gdzie:
- x, v – to dane (tworzące węzły) do których zostanie dopasowany model,
- xq – to liczba lub wektor wartości dla których zostaną obliczone nowe, odpowiadające mu wartości funkcji aproksymującej vq
- method – metoda interpolacji, np.: linear – liniowa, nearest – najbliższego sąsiada, pchip – wielomianem 3-go stopnia z ciągłą pierwszą pochodną, itp.
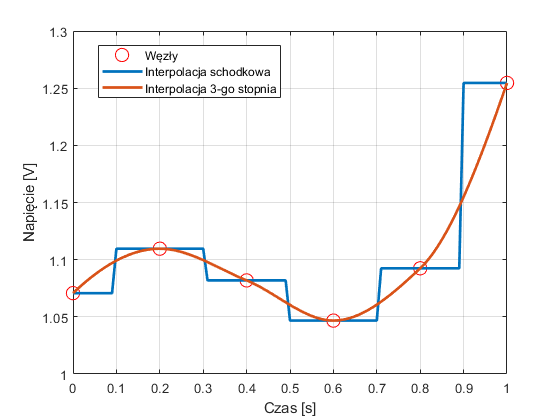
Użycie funkcji interp1 oraz porównanie metod interpolacji obrazuje poniższy przykład, do którego dane można pobrać tutaj.
clear all; close all; clc
load dane02 % wczytujemy dane pomiarowe z pliku
% Przygotowanie dwóch takich samych rysunków
figure(1); plot(t,y,'ro','MarkerSize',10);
xlabel('Czas [s]'); ylabel('Napięcie [V]');
grid on;
figure(2); plot(t,y,'ro','MarkerSize',10);
xlabel('Czas [s]'); ylabel('Napięcie [V]');
grid on;
%% Interpolacja
t2 = 0:0.01:1; % wektor argumentów dla których będą obliczane
% wartości funkcji interpolującej
% interpolacja liniowa
y2 = interp1(t,y,t2,'linear')
figure(1); hold on; plot(t2,y2,'LineWidth',2)
legend('Węzły', 'Interpolacja liniowa')
% interpolacja schodkowa
y3= interp1(t,y,t2,'nearest')
figure(2); hold on; plot(t2,y3,'LineWidth',2)
% interpolacja wielomianem 3-go stopnia
y4 = interp1(t,y,t2,'pchip')
plot(t2,y4,'LineWidth',2)
legend('Węzły','Interpolacja schodkowa', 'Interpolacja 3-go stopnia')
Ekstrapolacja (Extrapolation)
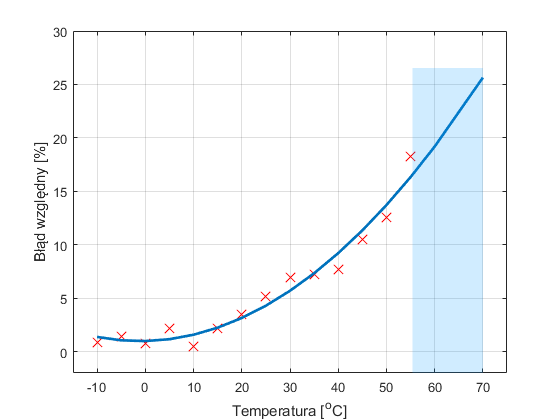
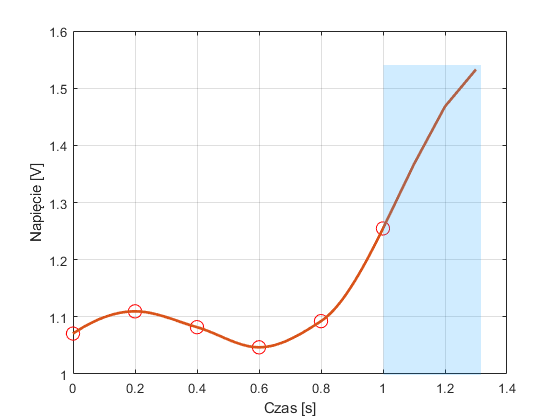
Ekstrapolacja polega na obliczeniu wartości modelu, który został dopasowany do danych, poza zakresem dla którego te dane zgromadzono. Jest to więc wyznaczanie wartości funkcji na zewnątrz przedziału, w którym wartości tej funkcji są znane. Ekstrapolację można przeprowadzić zarówno dla modelu aproksymującego dane pomiarowe, jak i po interpolacji. Ilustrują to poniższe rysunki, na których kolorem niebieskim zaznaczono obszary ekstrapolacji danych.
W jaki sposób wykonać ekstrapolację w MATLABie? Spróbujcie zrobić to sami. Dajcie znać w komentarzach czy się udało. Powodzenia!