Wiele osób, po pierwszym zetknięciu się z programem MATLAB, sądzi, że nazwa aplikacji musi mieć coś wspólnego ze słowem matematyka (mathematics). Nie jest to prawda. Nazwa powstała ze złożenia wyrazów MATrix i LABoratories. MATLAB został stworzony z myślą o wykonywaniu podstawowych operacji na macierzach i początkowo, właściwie nadawał się tylko do tego. Do dziś macierz jest podstawowym typem danych w środowisku, jednak program został w ciągu ostatnich dekad bardzo rozwinięty. Użytkownicy mają dostęp do tak wielu wyrafinowanych numerycznych procedur obliczeniowych, że o ile przetrzymywanie danych w macierzy wydaje się jak na razie całkiem naturalne, to sięganie po „prymitywne” matematyczne narzędzia operacji na macierzach jawi się jako kompletnie zbędne Tu można doszukiwać się przyczyny braku kojarzenia MATLABa z macierzą. No cóż, najczęściej tak właśnie jest, że „ręcznie” na macierzach operować nie musimy. Dobrze jednak pamiętać, że jakby co, to w MATLABie można. Warto też wiedzieć, w jaki sposób można, no i w końcu warto wiedzieć, w jaki powinno się pewne rzeczy robić.
Spróbujmy przy pomocy programu rozwiązać poniższy układ równań:
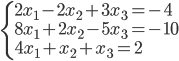
W zapisie macierzowym możemy to równanie przedstawić jak poniżej:
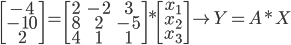
Aby rozwiązać równanie, należy obie strony równania przemnożyć z lewej przez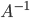 
. Wtedy otrzymujemy:
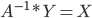
Jak za rozwiązanie problemu zabrać się w MATLABie? Należy zacząć od wprowadzenia danych:
A = [2 -2 3; 8 2 -5; 4 1 1] Y = [-4 -10 2]'
Teraz wprowadzamy formułę podaną powyżej, można to zrobić na dwa sposoby...
X = A^(-1) * Y X = inv(A) * Y
by otrzymać wynik:
X =
-1.0000
4.0000
2.0000
Wynik zdaje się w porządku, tylko skąd te liczne zera po kropce? Takie zera wskazują nam, że gdzieś tam, na którymś miejscu po przecinku, czego z racji ograniczenia liczby wyświetlanych znaków nie widać, pojawia się coś, co nie jest zerem. Mamy tu do czynienia z błędem numerycznym obliczeń, który jest nieodzownym wynikiem wykorzystywania do kalkulacji komputera o skończonej dokładności obliczeń. Czy więc możemy być usatysfakcjonowani wynikiem? Okazuje się, że nie musimy. Może spróbujmy wyznaczyć X nieco inaczej. Można przecież zapisać kluczową formułę matematyczną tak:
X = A\Y
Wynik wygląda wtedy nieco inaczej.
X =
-1
4
2
Wynik najlepszy, bo pozbawiony jakiegokolwiek numerycznego błędu obliczeniowego.
Operacji / oraz \ MATLAB nie interpretuje jako dzielenia. A\Y dla programu oznacza: odwróć macierz A i pomnóż przez Y. Operacja A/Y oznacza z kolei: macierz A pomnóż przez odwróconą macierz Y. Oczywiście, macierze mogą być czasem jednoelementowe i wtedy / oraz \ oznaczają po prostu: podziel. Dla danych, które mamy zdefiniowane w przestrzeni roboczej, ta operacja A/Y jest nie do wykonania
A/Y
Error using /
Matrix dimensions must agree.
Warto zauważyć, że komunikat błędu mówi o tym, że rozmiary macierzy muszą się zgadzać, nie ma nic o tym, że macierz Y powinna być kwadratowa...
Sprawdźmy, co się stanie, gdy do równania dopiszemy jeszcze jeden wiersz:
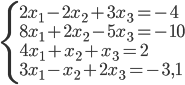
A = [2 -2 3; 8 2 -5; 4 1 1;3 -1 2] Y = [-4 -10 2 -3.1]' X = A\Y
X =
-1.0058
4.0106
1.9959
Co się stało? Skąd się wziął wynik? Okazuje się, że wyznaczane X jest takie, by zminimalizować błąd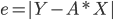 
Ma to oczywiście sens. W rzeczywistym świecie, badając zależności pomiędzy zmiennymi, dokonujemy licznych pomiarów z góry wiedząc, że nasze pomiary będą obarczone błędem. A MATLAB jest w końcu językiem obliczeń technicznych wykorzystywanym do rozwiązywania rzeczywistych problemów tego świata. Oczywiście, zawsze można sięgnąć po wygodne narzędzia zawarte w modułach rozszerzających, takich jak Statistics and Machine Learning Toolbox czy Curve Fitting Toolbox, ale warto pamiętać, że w samym MATLABie też można wiele zdziałać.
A dlaczego wynik działania komendy X = A\Y jest bardziej dokładny niż X = inv(A) * Y? W dokumentacji funkcji inv jest napisane, że to zasługa używania eliminacji Gaussa, możesz napisać coś więcej na ten temat?
Polecenie A\Y jest w matlabie równoważne wywołaniu funkcji lmdivide(A,Y).
W przypadku inv(A)*Y mamy dwie niezależne operacje, tj. odwracanie macierzy, co wiąże się z pewnym błędem, a następnie mnożenie wyniku przez Y. W przypadku lmdivide(A,Y) algorytm działa inaczej. Po szczegóły odsyłam do dokumentacji.
http://www.mathworks.com/help/matlab/ref/mldivide.html