Rozwiązywanie równań różniczkowych w MATLABie
Od kilku dni dostępna jest wersja 2016b MATLABa. Tym razem zmiany koncentrują się głównie na obszarze „Big Data”. Wśród nowinek znalazła się jednak jedna, która - choć wcale nie spektakularna - może znacznie ułatwić codzienną pracę każdemu użytkownikowi. Chodzi o wprowadzenie możliwości definiowania funkcji w obrębie skryptu. Przy próbie policzenia czegoś na szybko może to być bardzo pomocne – przykładem niech będzie numeryczne rozwiązywanie równań różniczkowych.
W MATLABie równania różniczkowe możemy rozwiązywać w sposób symboliczny, do czego niezbędny jest Symbolic Math Toolbox oraz metodą numeryczną, do czego wystarczy podstawowa wersja programu. Jest jeszcze Partial Differential Equation Toolbox, służący do rozwiązywania równań różniczkowych cząstkowych. Ten wpis poświęcony jest rozwiązywaniu równań (i układów równań) różniczkowych z pomocą „gołej” wersji MATLABa.
W celu rozwiązania równania różniczkowego w MATLABie można posłużyć się funkcją z rodziny odeX (za ODE stoi Ordinary Differential Equation), np. ode45. Cyfry na końcu wskazują na to, jaki solver zostanie wykorzystany do obliczeń.
Podstawowa składnia funkcji ode45 (i pokrewnych) jest następująca:
ode45(odefun,tspan,y0)
Patrząc od tyłu, mamy następujące argumenty wejściowe:
- y0 – warunki początkowe,
- tspan – przedział t dla jakiego dokonujemy obliczeń,
- odefun – uchwyt do funkcji, dla której rozwiązanie chcemy znaleźć.
Więcej o uchwytach do funkcji można znaleźć w jednym z moich poprzednich wpisów.
W końcu mogę wyjaśnić, co ma piernik do wiatraka, tzn. co mają zmiany wprowadzone w nowej wersja MATLABa do rozwiązywania równań różniczkowych. Dotychczas szukając rozwiązania takiego równania trzeba było najczęściej tworzyć dwa pliki tj. skrypt główny wywołujący funkcję odeX oraz plik z definicją funkcji (odefun.m). Można było co prawda w niektórych przypadkach posłużyć się funkcją anonimową lub zamiast głównego skryptu stworzyć funkcję i dopisać do niej subfunkcję, jednak możliwość stworzenia skryptu i funkcji w jego obszarze ogólnie zwiększa czytelność rozwiązania. Mała rzecz, a cieszy! Najlepiej zilustrować sprawę przykładem.
Równanie na start
Rozważmy najprostszy model rozrostu populacji danego gatunku. Jeśli przyjmiemy, że rozrost może być absolutnie niczym nieograniczony, to model matematyczny będzie wyglądał następująco:
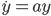
y określa wielkość populacji w danym czasie, stała a określa szybkość namnażania się osobników.
Przyjmijmy, że a = 1 i "przepiszmy" problem do MATLABa tworząc nowy skrypt.
ode45(@odefun, [0 4], 2); function dydt = odefun(t,y) dydt = y; %równanie dy(t)/dt = y(t) end
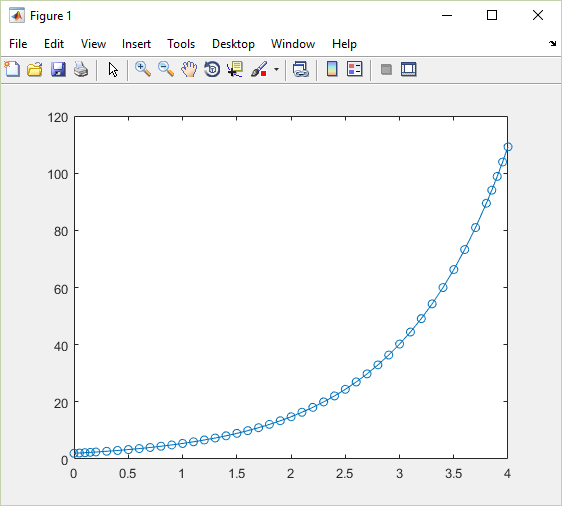
Równanie trafiło do bloku function (w przypadku starszych wersji MATLABa trzeba utworzyć osobny plik), a za jego rozwiązanie i utworzenie wykresu odpowiedzialna jest funkcja ode45
Przejdźmy do bardziej złożonego modelu ofiara – drapieżnik, równania Lotki-Volterry.
Układ równań różniczkowych
Na model składa się nie jedno, a dwa równania różniczkowe:
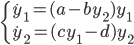
Przy pierwszym podejściu dla uproszczenia załóżmy, że wszystkie parametry (a,b,c,d) wynoszą 1. By rozwiązać problem musimy zapisać funkcję odefun w taki sposób, wy zwracała wektor zamiast pojedynczej wartości. Również wywołując funkcję ode45 należy pamiętać, że mamy do czynienia z układem równań. Warunki początkowe należy zdefiniować w formie wektora (tzn. podać wartość zarówno dla y1 jak i y2).
[t,y] = ode45(@odefun, [0 4], [10 2]); %populacja początkowa ofiar: 10, drapieżników: 2
plot(t, y); % tym razem funkcja ode45 zwróciła argumenty wyjściowe i wykres nie został wygenerowany automatycznie
legend({'populacja ofiar'; 'populacja drapieżników'});
function dydt = odefun(t,y)
dydt = [(1 - y(2)) * y(1);...
(y(1) - 1)* y(2)];
end
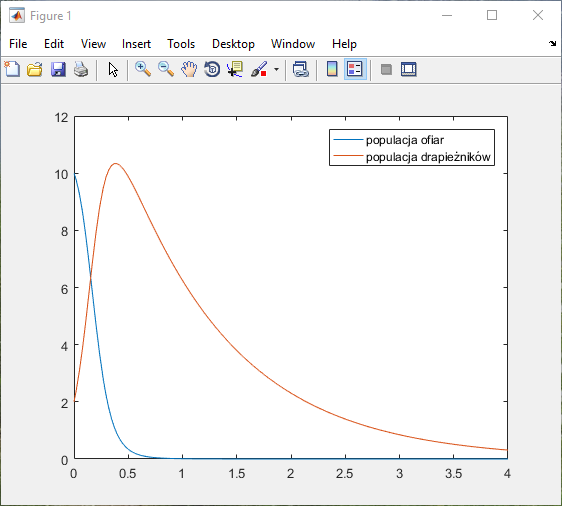
W rzeczywistości rozwiązując równanie chcemy określić gamę parametrów dodatkowych. Można je oczywiście ustawić „na sztywno” w bloku funkcji ale o wiele lepszym pomysłem jest ich przekazanie w momencie uruchamiania metody ode45
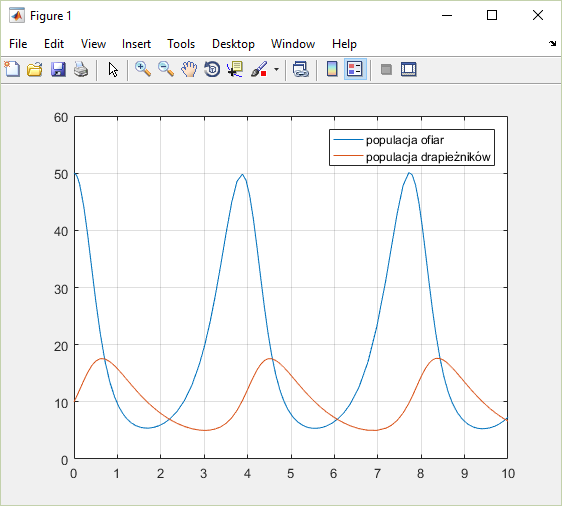
params = [3 0.3 0.05 1];
[t, y] = ode45(@odefun, [0 10], [50 10], [], params);
plot(t, y); grid('on');
legend({'populacja ofiar'; 'populacja drapieżników'})
function dydt = odefun(t,y, params)
dydt = [(params(1) - params(2)*y(2)) * y(1);...
(params(3)*y(1) - params(4))* y(2)];
end
To wszystko oczywiście nie wyczerpuje w pełni tematu, cdn…

Bardzo się cieszę, że znalazł pan czas na podzielenie się swoją wiedzą. Dzięki panu jestem mądrzejszy o parę cennych rozwiązań. Pozdrawiam i życzę owocnych badań, Michał
Witam,
mam pytanie, jak wygląda model lotki Volterry zmodyfikowany o wpływ konkurencji o pożywienie?
dx/dt=(a-by)x-ex
dy/dt=(cx-d)y-fy
Pozdrawiam
Cześć,
możesz podać więcej informacji?