Dlaczego Simulink – przykład
(kontynuacja wpisu poprzedniego)
Gotowe Simulinkowe modele wykorzystane w tym wpisie są dostępne na stronie MATLAB Central. (Załączona prezentacja jest w języku hebrajskim, jednak opisy modeli są po angielsku).
Wyobraźmy sobie dosyć ambitne zadanie, jakim jest zaprogramowanie systemu sterowania kosmicznego lądownika. Sytuacja przedstawia się następująco: z kosmosu w stronę Ziemi zmierza lądownik. Naszym zadaniem jest opracowanie systemu sterowania, który będzie sterował pracą silników w taki sposób, by obiekt wylądował bezpiecznie na powierzchni planety. Jak zabrać się za takie zadanie? Można oczywiście zbudować kilka prototypowych lądowników, wynieść je w kosmos i posyłać kolejno w stronę Ziemi, na gorąco sprawdzając pomysły na najlepszy system sterowania. Lepszym rozwiązaniem jest jednak budowa matematycznego modelu obiektu, na którym bezpiecznie będzie można testować różne koncepcje sterowania. Simulink stworzony został właśnie w takim celu.
Uproszczony model obiektu
Uniwersalna zasada jest taka, że zacząć należy od uproszczonego modelu. Na początku załóżmy, że obiekt opada swobodnie, a jedyna siła, która na niego działa, to siła grawitacji. Wychodzimy od znanego wszystkim równania
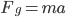
Równanie można uprościć i zapisać tak:
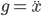
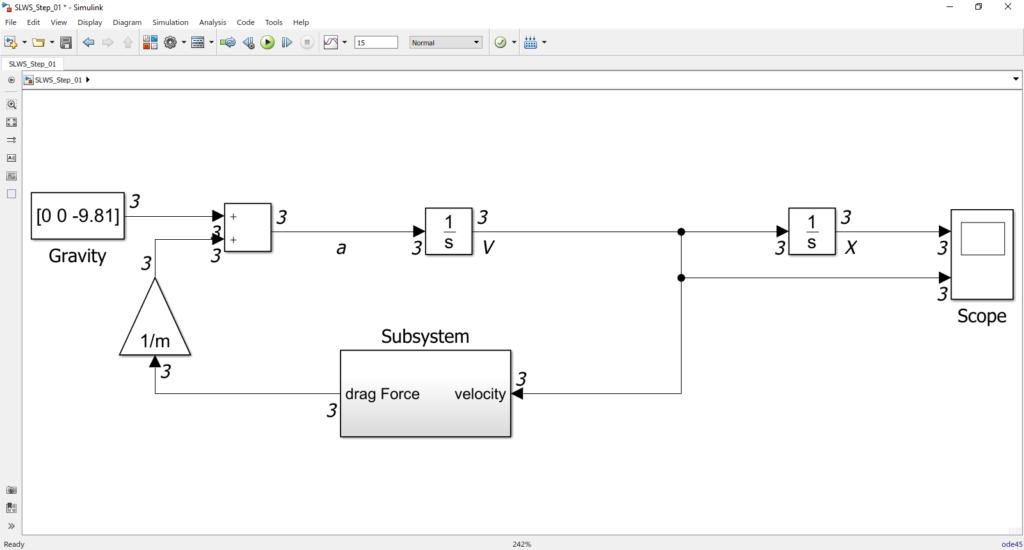
Interesuje nas położenie i prędkość opadania lądownika, informacje te możemy uzyskać rozwiązując powyższe równanie. Aby zrobić to w Simulinku, należy stworzyć odpowiedni diagram blokowy.
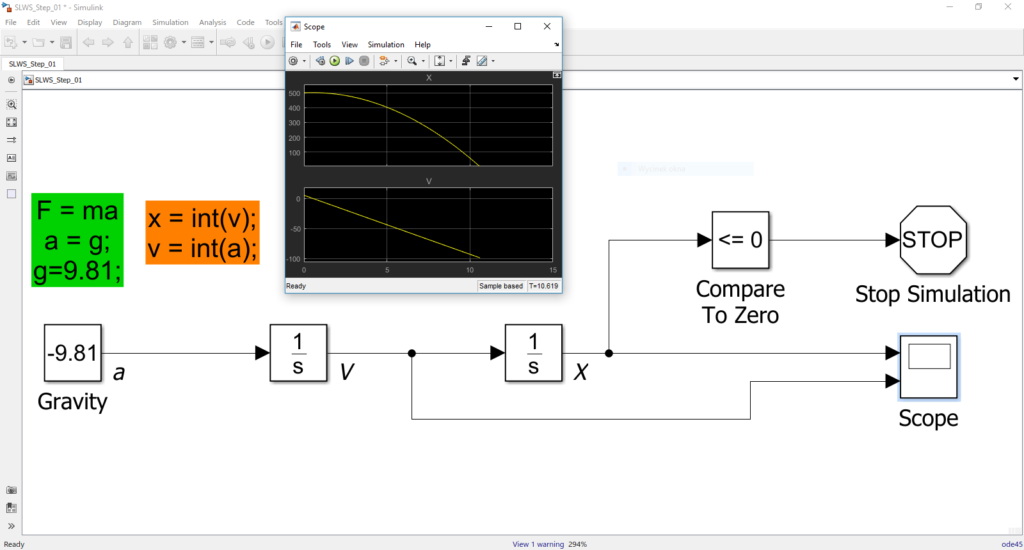
Wychodzimy od przyspieszenia ziemskiego, następnie całkujemy, by wyznaczyć prędkość. Całkując prędkość otrzymujemy informacje o położeniu. Dodatkowe dwa widoczne bloki sprawiają, że symulacja zatrzyma się, gdy położenie osiągnie wartość 0, czyli gdy lądownik zetknie się z Ziemią. Warunki początkowe (startowa wysokość 500m) zostały wprowadzone jako parametry w bloku/blokach całkowania.
Stworzenie całej symulacji zajmuje dosłownie kilka chwil, jednak na tym etapie jak najbardziej zrozumiałe pozostaje pytanie: dlaczego Simulink? Taką symulację równie łatwo można by zrealizować bezpośrednio w MATLABie, a w zasadzie w ogóle nie potrzeba tu wspomagania komputerowego. Rzeczywiście, na tym etapie „problem” może rozwiązać absolwent gimnazjum uzbrojony w kartkę i długopis, jednak w kolejnych krokach model zostanie rozbudowany i rozwiązanie nie będzie już takie proste.
Rozbudowa modelu
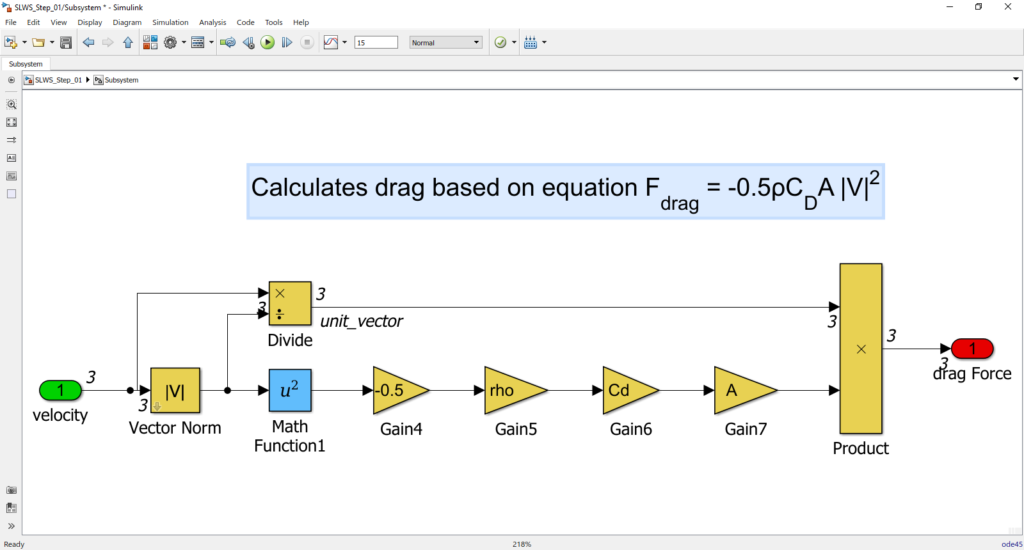
Dość popularny jest mit, jakoby prędkość opadania obiektu nie zależała od jego masy. W rzeczywistości wystarczy spojrzeć na równanie, które uwzględnia opór powietrza, by zdać sobie sprawę, że masa odgrywa swoją rolę.
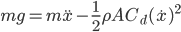
Rozwiązanie powyższego równania na kartce papieru może stanowić pewne wyzwanie, złożenie odpowiedniego schematu w Simulinku jest dosyć proste.
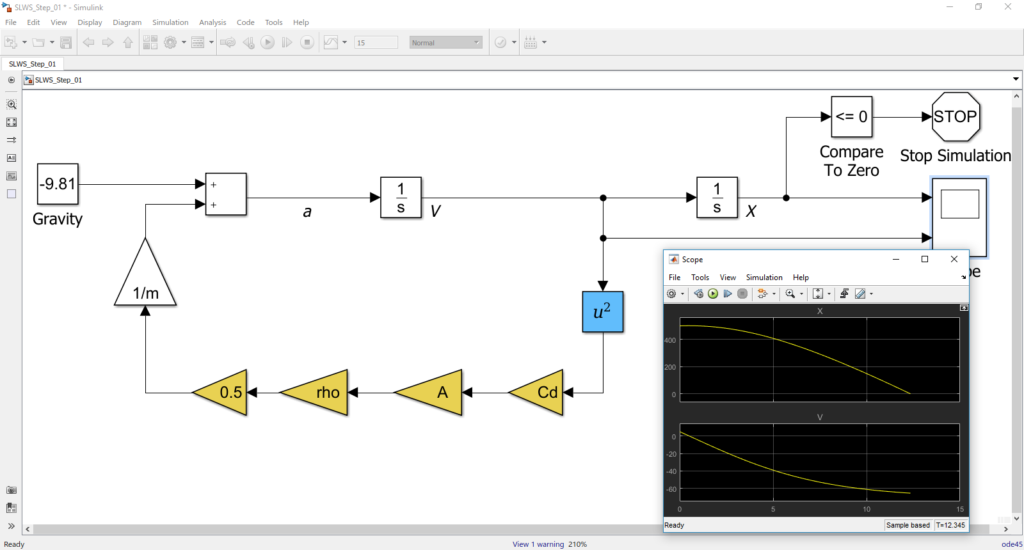
Nie chodzi bynajmniej o to, że Simulink zwalnia nas z konieczności znajomości metod rozwiązywania równań różniczkowych. Chodzi raczej o to, że poszukując rozwiązania problemu czasami lepiej jest pewne rzeczy poddać symulacji, niż poświęcać czas na poszukiwania rozwiązania analitycznego.
Dalsza rozbudowa modelu
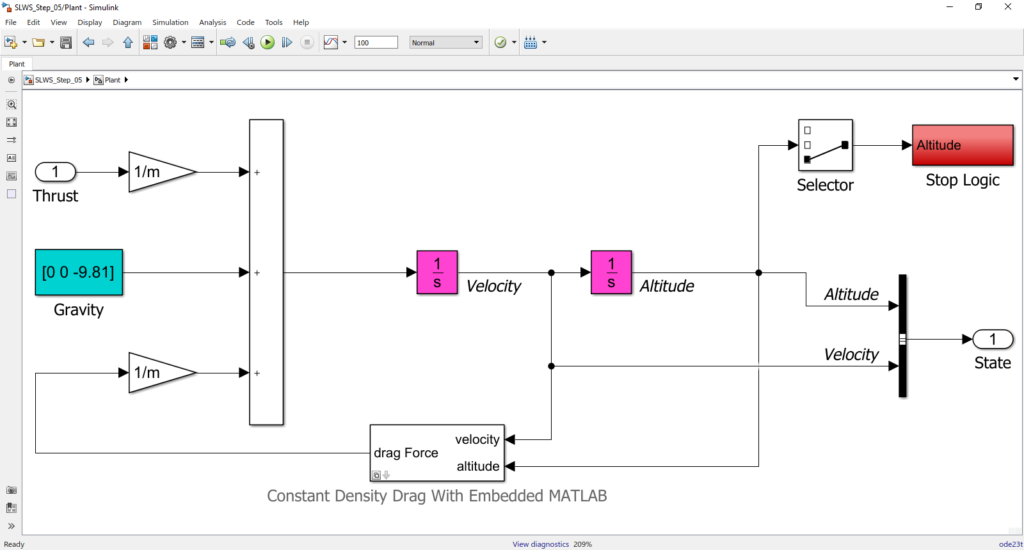
W rzeczywistości interesuje nas położenie obiektu nie w jednym, a w trzech wymiarach. Modyfikacja nie jest trudna, lecz w celu zwiększenia czytelności modelu dobrze będzie część toru przetwarzania zamknąć w osobnym bloku, tworząc podsystem.
Tu dochodzimy do kolejnej zalety stosowania Simulinka. Jest to czytelność stosowanych rozwiązań. Oczywiście, modele w Simulinku mogą być bardzo rozbudowane i skomplikowane, jednak możliwość tworzenia niezależnych podsystemów sprawia, że prawidłowo stworzony model może być zawsze zrozumiały. A w każdym razie konkretny wycinek modelu będzie zrozumiały dla inżyniera, który się nim zajmuje.
Wykorzystanie blocksetów
Czy można na tym poprzestać? Wszystko zależy od tego, jaki dokładny chcemy mieć model. W formule, która jest podstawą do budowy modelu, występuje cały szereg współczynników, które warto rozszyfrować. 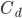 to współczynnik oporu,
to współczynnik oporu, 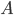 to powierzchnia obiektu a
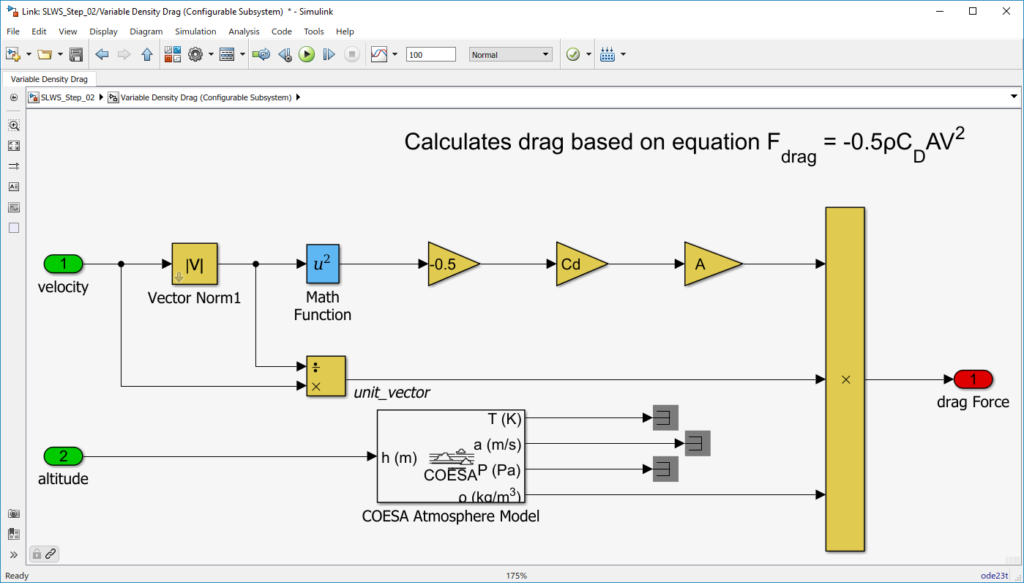
to powierzchnia obiektu a  to gęstość powietrza. Ziemska atmosfera jest złożona i przyjęcia stałej wartości tego ostatniego współczynnika to duże uproszczenie. Jeśli chcielibyśmy zwiększyć dokładność modelu należałoby zbudować model oddający zmianę gęstości powietrza w zależności od wysokości. Okazuje się, że nie wszystko w Simulinku trzeba robić samodzielnie, czasami można znaleźć gotowe rozwiązanie w dołączanych do pakietu Simulink blocksetach.
to gęstość powietrza. Ziemska atmosfera jest złożona i przyjęcia stałej wartości tego ostatniego współczynnika to duże uproszczenie. Jeśli chcielibyśmy zwiększyć dokładność modelu należałoby zbudować model oddający zmianę gęstości powietrza w zależności od wysokości. Okazuje się, że nie wszystko w Simulinku trzeba robić samodzielnie, czasami można znaleźć gotowe rozwiązanie w dołączanych do pakietu Simulink blocksetach.
Wykorzystanie modelu
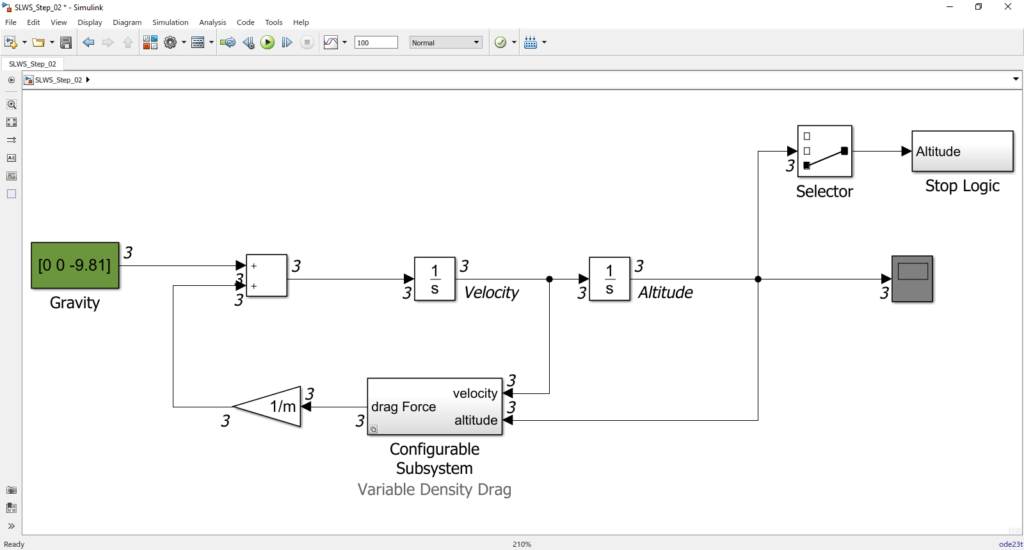
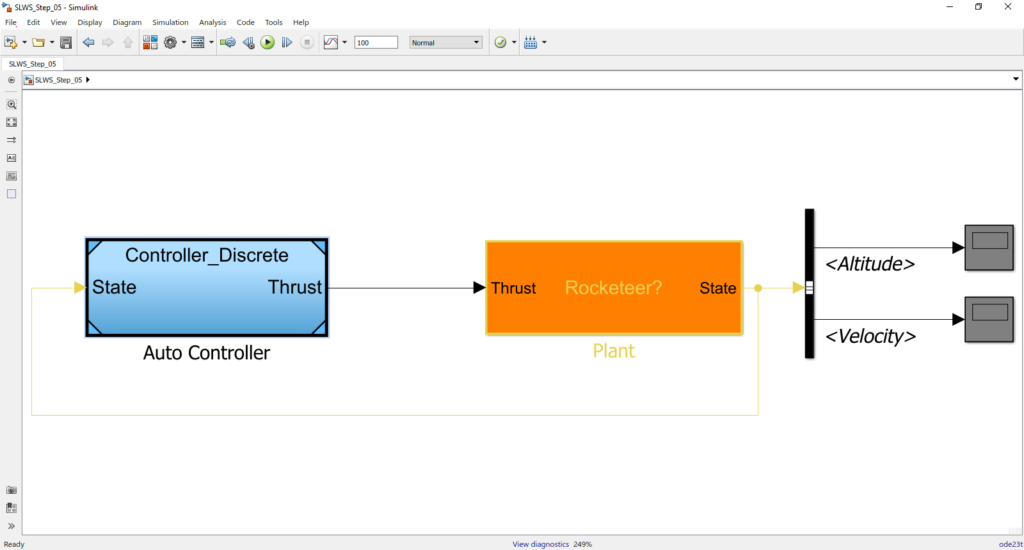
W momencie, w którym model jest wystarczająco dobry, można w końcu zrobić z niego pożytek. W tym wypadku będzie to zaprojektowanie systemu sterowania silnikami, które będą kontrolować opadanie lądownika. Początkowa modyfikacja sprowadza się do tego, że na wejściu modelu pojawia się dodatkowa linia - siła pochodząca od silników. To jak modelowane będą silniki, to już w zasadzie osobna historia.
Powyżej gotowy szkielet zamkniętego układu sterowania. Pozostaje tylko zaprojektowanie systemu i optymalizacja jego parametrów.
Podsumowanie
Simulink to środowisko do modelowania systemów dynamicznych. Biorąc pod uwagę przedstawiony przykład, powyższe zdanie nie powinno być już zagadkowe. Proces modelowania jest szybki oraz czytelny - to główna zaleta narzędzia i jego przewaga nad alternatywnymi rozwiązaniami. Simulink to jednak nie tylko modelowanie. Korzystając z opracowanych w środowisku modeli można wygenerować kod C, by zaprojektowane rozwiązanie przenieść na rzeczywiste urządzenie. Więcej informacji na temat środowiska Simulink znajdziecie w webinarium Wprowadzenie do Simulinka, dostępnego na stronach firmy ONT.