Transformacja Fouriera
Transformata Fouriera to jedno z podstawowych narzędzi dostępnych w MATLABie. Bardzo często użytkownicy błędnie łączą najpopularniejszą funkcję związana z transformacją Fouriera (fft – fast Fourier transform) z przybornikiem Signal Porcessing Toolbox. W rzeczywistości funkcja fft jest częścią podstawowego pakietu MATLAB. Jest to w końcu naprawdę "podstawowa" funkcja i prawdopodobnie dla wielu użytkowników będzie dosyć toporna w użyciu. Wiąże się to z koniecznością „obrobienia” wyników zwracanych przez fft w przypadku najpopularniejszych zastosowań. Korzystając z Signal Processing Toolbox możemy liczyć na pewne ułatwienia. Funkcje takie jak periodogram czy pwelch zwracają nam wyniki w przyjaźniejszej postaci. Nie będę się w tym wpisie zagłębiać w temat działania powyższych funkcji. Chciałbym natomiast przedstawić, w jaki sposób MATLAB pomógł mi swojego czasu zrozumieć, o co w tej całej transformacji Fouriera tak naprawdę chodzi.
Prawdopodobnie wywód powinienem rozpocząć od przedstawienia kilku matematycznych formuł związanych z szeregiem Fouriera, ale tak szczerze, to nie bardzo uśmiecha mi się tracić czasu na wklepywanie wszystkiego w TEXu, nie jestem w tym biegły. No i w końcu można zawsze odesłać zainteresowanych do Wikipedii. Z kolei druga część wpisu dotycząca interpretacji transformacji Fouriera i FFT jest dostępna TUTAJ.
Skoncentruję się na esencji, całkowym przekształceniu Fouriera.
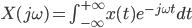
Dzięki tej cudownej formule możemy zmieniać postrzeganie funkcji z takiego:
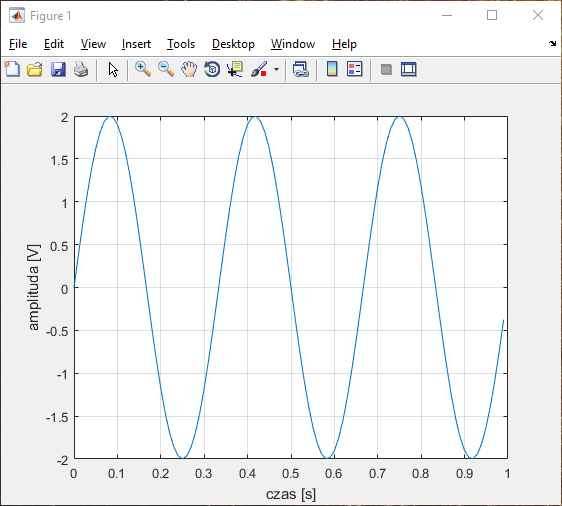
na taki:
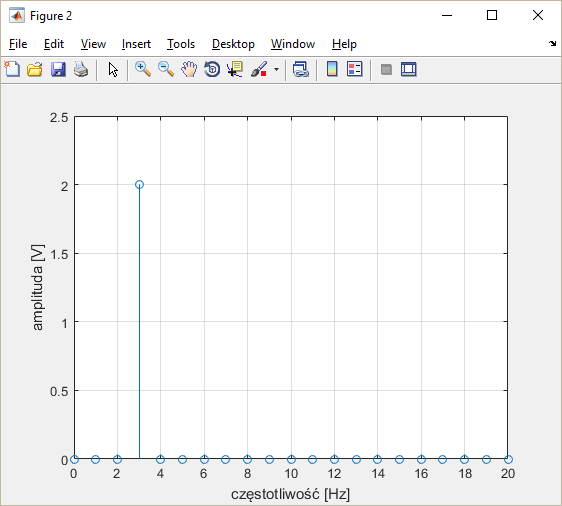
Pytanie jest jedno: jak to możliwe?
Cała idea przedstawiona przez Fouriera sprowadza się do tego, że możemy sobie wziąć dowolny, rzeczywisty przebieg (są pewne ograniczenia) i przedstawić go jako sumę sinusów i cosinusów o różnych amplitudach. Jak się przyglądniemy przebiegom niektórych funkcji, to nawet na oko widać, że składają się one właśnie z podstawowych funkcji sinusoidalnych. Weźmy na przykład dwie funkcje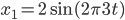
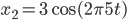
i je zsumujmy. Otrzymamy przebieg jak przedstawiony poniżej.
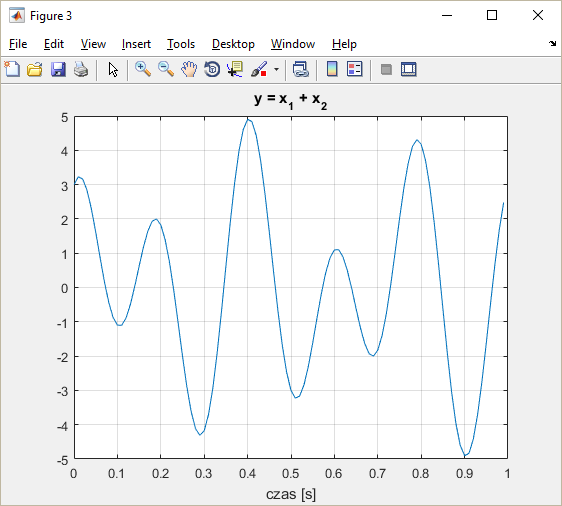
Operując szeregiem złożonym z 50 kolejnych funkcji sinus możemy nawet stworzyć przebieg zbliżony do przebiegu prostokątnego.
%% wektor czasu
dt = 0.001;
t = 0:dt:2-dt;
%% szereg amplitud i częstotliwości
fs = 1:2:99;
As = 1./fs;
%% generowanie sygnału
z = As*sin(2*pi*fs'*t);
%% wykres
plot(t, z); xlabel('czas [s]');
title('$ $z(t) = \sin 2\pi t + \frac{1}{3}\sin 2\pi 3t + \frac{1}{5}\sin 2\pi 5t + ...$ $','interpreter','latex')
grid on
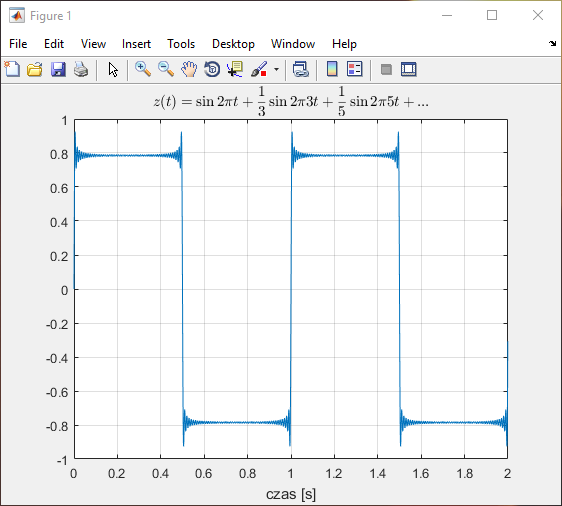
Pięknie to działa w jedną stronę, to znaczy sumując funkcje sinusoidalne o różnych amplitudach i częstotliwościach możemy otrzymać przeróżne funkcje wynikowe, ale zastanówmy się, czy da się do tego podejść z drugiej strony. To znaczy, dany jest przebieg wynikowy i mamy powiedzieć, jakie funkcję podstawowe się na niego złożyły. Może się to wydawać niemożliwe. Przecież, jeśli zsumujemy 3 i 5 to wychodzi nam, 8 ale jeśli mielibyśmy powiedzieć, skąd się wzięło się 8 (tzn. rozwiązać równanie 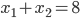 ), to odpowiedzi jest kilka…. Okazuje się, że jeśli badamy wynik sumowania funkcji, sytuacja nie jest taka beznadziejna.
), to odpowiedzi jest kilka…. Okazuje się, że jeśli badamy wynik sumowania funkcji, sytuacja nie jest taka beznadziejna.
Przyglądnijmy się funkcji 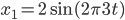
Co się stanie, jeśli funkcję 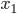 „przemnożymy” przez
„przemnożymy” przez 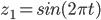 ? Mnożenie dwóch funkcji rozumiem tu jako całkowanie iloczynu,
? Mnożenie dwóch funkcji rozumiem tu jako całkowanie iloczynu, 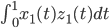 . Jeśli przeniesiemy to zadanie do świata cyfrowego, to operacja może wyglądać tak:
. Jeśli przeniesiemy to zadanie do świata cyfrowego, to operacja może wyglądać tak:
dt = 0.01; t = 0:dt:1-dt; x1 = 2*sin(2*pi*3*t); z1 = sin(2*pi*t); sum(x1.*z1)
ans =
2.1878e-14
W wyniku otrzymujemy 0 (z drobnym błędem). Ten sam wynik otrzymamy również, jeśli przemnożymy 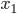 przez
przez 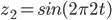 i
i 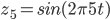 . W zasadzie jedyna szansa na nie otrzymanie 0 pojawia się wtedy, gdy przemnożymy
. W zasadzie jedyna szansa na nie otrzymanie 0 pojawia się wtedy, gdy przemnożymy 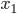 przez funkcję sinusoidalną o tej samej częstotliwości (
przez funkcję sinusoidalną o tej samej częstotliwości (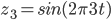 ).
).
x1 = 2*sin(2*pi*3*t); z3 = sin(2*pi*3*t); sum(x1.*z3)
ans =
100
Wartość wynikowa jest całkiem spora, ale w tym momencie ważne jest to, że nie jest zerem.
Wróćmy do funkcji 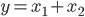 i ją przemnóżmy przez
i ją przemnóżmy przez 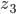 . Okazuje się, że wynik jest taki sam, jak powyżej…
. Okazuje się, że wynik jest taki sam, jak powyżej…
x1 = 2*sin(2*pi*3*t); x2 = 3*cos(2*pi*5*t); y = x1 + x2; z3 = sin(2*pi*3*t); sum(x1.*z3)
ans =
100
Wniosek jest taki, ze "mnożąc" funkcję badaną przez podstawową funkcję sinusoidalną możemy odkryć, czy trafiliśmy na jedną ze składowych. Najpewniej byłoby przetestować wszystkie możliwe częstotliwości i wynik zobrazować na wykresie. W zasadzie, w wersji "analogowej" można to zapisać tak:
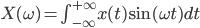
„Lecimy” po kolejnych częstotliwościach 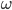 i wszystko gra. Jednak z jakichś względów formuła całkowego przekształcenia Fouriera wygląda inaczej. Aby to wyjaśnić, sprawdźmy, co się stanie, gdy przemnożymy funkcję
i wszystko gra. Jednak z jakichś względów formuła całkowego przekształcenia Fouriera wygląda inaczej. Aby to wyjaśnić, sprawdźmy, co się stanie, gdy przemnożymy funkcję 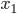 przez funkcję
przez funkcję 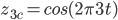
x1 = 2*sin(2*pi*3*t); z3c = cos(2*pi*3*t); sum(x1.*z3c)
ans =
-8.2712e-15
Wynik to 0. Funkcja 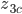 jest przesunięta w fazie względem funkcji
jest przesunięta w fazie względem funkcji 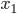 o
o 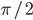 . Jak wygląda sytuacja, gdy przemnożymy funkcję
. Jak wygląda sytuacja, gdy przemnożymy funkcję 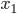 przez funkcję sinusoidalną o tej samej częstotliwości, lecz przesuniętą względem niej o jakąś inną wartość, np.
przez funkcję sinusoidalną o tej samej częstotliwości, lecz przesuniętą względem niej o jakąś inną wartość, np. 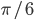 ?
?
x1 = 2*sin(2*pi*3*t); z3fi = sin(2*pi*3*t + pi/6); sum(x1.*z3fi)
ans =
86.6025
Wynik nie jest zerem, choć jest mniejszy od 100. Wygląda na to, że oprócz częstotliwości funkcji składowej trzeba wziąć pod uwagę również jej przesunięcie fazowe. Nie musimy jednak sprawdzać wszystkich możliwych przesunięć z przedziału 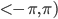 , wystarczy sprawdzić, na ile badana funkcja jest "podobna" do sinusa, a na ile do kosinusa. Istotna będzie wypadkowa.
, wystarczy sprawdzić, na ile badana funkcja jest "podobna" do sinusa, a na ile do kosinusa. Istotna będzie wypadkowa.
z3fi = 2*sin(2*pi*3*t + pi/6); z3s = sin(2*pi*3*t); z3c = cos(2*pi*3*t); s = sum(z3s.*z3fi); c = sum(z3c.*z3fi); sqrt(s^2 + c^2)
ans =
100
Wygląda na to, że wszystko się tym razem zgadza. Właśnie uwzględnienie możliwości przesunięcia w fazie poszczególnych składowych sygnału jest powodem, dla którego formuła całkowego przekształcenia Fouriera wygląda tak, a nie inaczej. Możemy przecież zapisać ją na dwa sposoby:
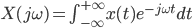
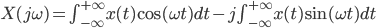
Można powiedzieć, że zmienna zespolona została wykorzystana w formule po to, by ładnie zapisać wzór i pogrupować dane. Koniec końców, to, co obserwujemy na wykresie charakterystyki amplitudowej sygnału, to 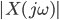
Wracając do początku, procedura "badania" sygnału z wykorzystaniem funkcji fft wygląda następująco:
dt = 0.01;
t = 0:dt:1-dt;
x1 = 2*sin(2*pi*3*t);
x2 = 3*cos(2*pi*5*t);
y = x1 + x2;
Y = fft(y); % wynik w postaci zespolonej
fp = 1/dt;
N = length(t);
df = fp/N;
f = 0:df:fp-df;
YY = (2/N)*abs(Y); %wyznaczenie wartości bezwględnej i skalowanie
stem(f, YY); xlim([0 20]); xlabel('częstotliwość [Hz]');
grid on;
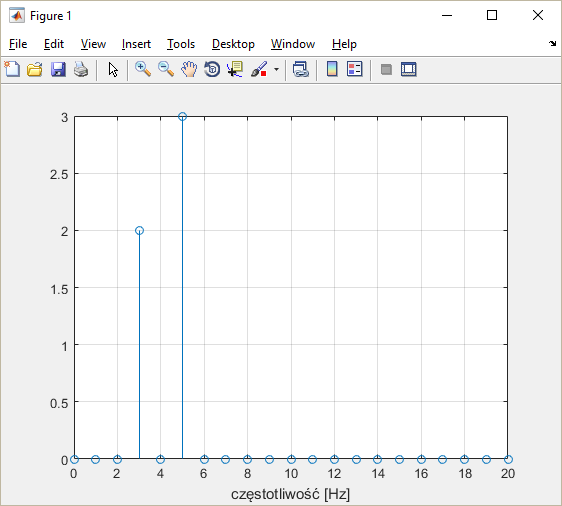
Temat jest oczywiście złożony i może się wydawać, że potraktowałem go w prostacki sposób. W zasadzie, to chyba tak właśnie jest. Niektórym wystarczy jedno spojrzenie na matematyczną formułę, by zrozumieć, jaka idea za nią stoi, jednak większość śmiertelników potrzebuje dodatkowych tłumaczeń. Mam nadzieję, że im ten wpis ułatwi zrozumienie.
Dalszy ciąg dotyczący transformacji Fouriera i jej interpretacji znajdziecie w kolejnym wpisie TUTAJ.
Zainteresowanym poważnym i jednocześnie czytelnym potraktowaniem tematu (liczne przykłady w MATLABie) polecam podręcznik „Cyfrowe przetwarzanie sygnałów” profesora Tomasza P. Zielińskiego.

Primo - FFT to nie jest transformacja Fouriera lecz jedna z jej szybkich implementacji dla systemów dyskretnych. Secundo - równie prosto mozna wytłumaczyć, iż transformacja Fouriera opiera sie o wykorzystanie splotu funkcji.
Świetny wpis 😉 Krótko, przejrzyście i na temat.
Linijka 17 ostatniego listingu:
zamiast Yabs powinno być YY.
Rzeczywiście, poprawiam.
Super wytłumaczenie, dzięki!