Uchwyty do funkcji, funkcje anonimowe
Jak wejść w temat tak, żeby za szybko nie rozbolała głowa? Na pewno nie polecam rozpoczynać od lektury teoretycznie powiązanego z tematem wpisu na Wikipedii. Najlepszym sposobem na wprowadzenie do tematu jest pokazanie sensownego przykładu i tak spróbuję rozegrać to tym razem. Rozpocznę od obliczenia przy pomocy MATLABa następującej całki:
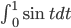
Z tą sensownością przykładu to oczywiście przenośnia, chodzi o to, by jak najprościej pokazać, jak w MATLABie ugryźć problem tego typu. Po krótkich poszukiwaniach pod hasłem integral w dokumentacji programu okazuje się, że jest funkcja, która może pomóc w rozwiązaniu problemu. Funkcja ma następującą składnie:
q = integral(fun,xmin,xmax)
Funkcja przyjmuje trzy argumenty wejściowe, dwa ostanie (xmin, xmax) określają przedział całkowania, natomiast pierwszy argument to… funkcja. Mamy tu sytuacje, gdzie argumentem wejściowym funkcji jest inna funkcja. W kontekście funkcji wyznaczającej całkę wydaje się to całkiem logiczne. Trzeba tylko wiedzieć, jak ten argument wejściowy odpowiednio przekazać i tu właśnie przydać się może uchwyt do funkcji. W najprostszej formie uchwyt do funkcji tworzy się w ten sposób, że przed nazwą funkcji wstawiany jest symbol @. Zatem rozwiązanie powyższego problemu będzie wyglądać tak:
q = integral(@sin, 0, 1)
q =
0.4597
Zazwyczaj jednak, jeśli przychodzi nam obliczyć całkę, to nie ma ona takiej podstawowej formy. Co w takim wypadku? Pierwszy sposób polega na zapisaniu własnej funkcji w formie m-pliku. Dla funkcji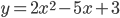 
można stworzyć plik o nazwie mojafunkcja.m prezentujący się następująco:
function y = mojafunkcja(x) y = 2*x.^2 - 5*x + 3;
Można teraz wywołać funkcję integral:
q = integral(@mojafunkcja, 0, 1)
q =
1.1667
Rozwiązanie nie wydaje się wygodne – tworzenie osobnego pliku w celu wyznaczenia całki z prostej w sumie funkcji co sporo ceregieli. I w tym momencie warto sięgnąć po funkcje anonimowe. Funkcje możemy przypisać do zmiennej a następnie przekazać do funkcji integral w następujący sposób:
y = @(x)2*x.^2 – 5*x + 3 integral(y, 0, 1); %y jest już zdefiniowany jako funkcja anonimowa, znak @ nie jest więc potrzebny
Funkcja anonimowa nie musi być funkcją jednej zmiennej. W nawiasie, po znaku @, możemy podać całą ich listę. Np.
f = @(x,y)x + x*y + y;
Tworząc przepis realizowany przez funkcję anonimową można również wykorzystać wbudowane jak i własne funkcje. Nic nie stoi na przeszkodzie, by funkcja przyjęła taką postać:
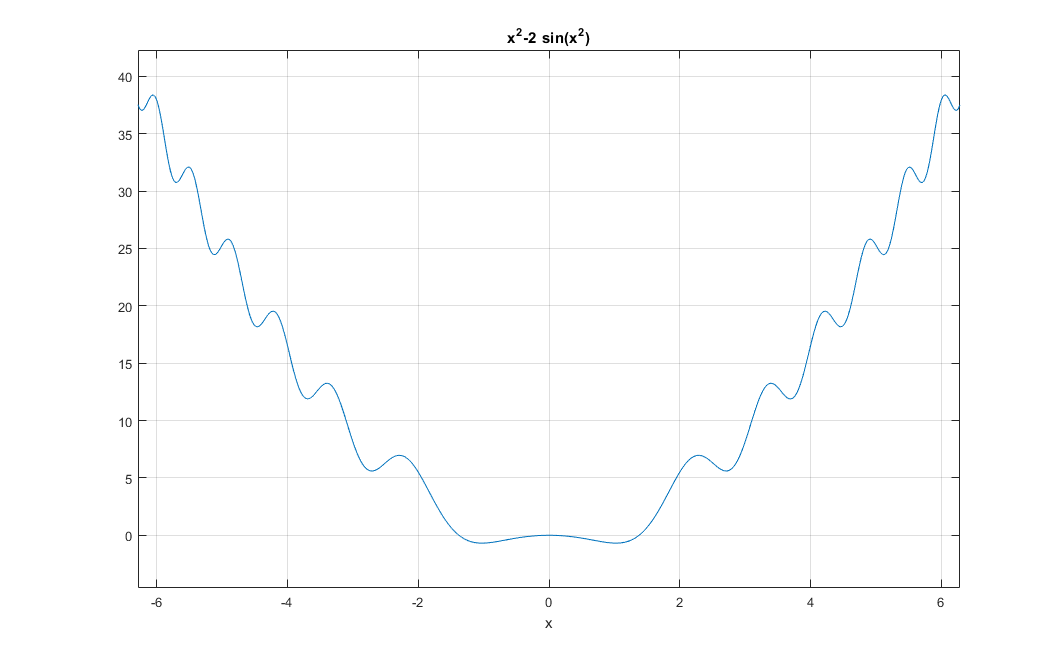
f = @(x)x.^2 - 2*sin(x.^2)
Gdyby kogoś ciekawiło, jak wygląda przebieg takiej funkcji, można posłużyć się funkcją fplot.
fplot(f)
W MATLAbie jest wiele funkcji, które jako argument mogą przyjąć inne funkcje (czy raczej uchwyty do innej funkcji). Warto na pewno wspomnieć o fzero, która umożliwia znalezienia miejsca zerowego wskazanej funkcji.
Umiejętne operowanie uchwytami do funkcji jest niezbędne do prawidłowego posługiwania się klasą timer oraz do rozwiązywania układów równań różniczkowych. Te tematy są jednak na tyle złożone, że zasługują na osobne wpisy.