MATLAB całkowanie numeryczne, to drugi po różniczkowaniu temat, który jest postrzegany jako trudny. Tym czasem po bliższej analizie okazuje się, że nie jest tak źle. MATLAB ma wbudowane funkcje służące do obliczania całek. Z tego artykułu dowiecie się jakie są podstawy teoretyczne całkowania numerycznego i jak to zrobić w MATLABie.
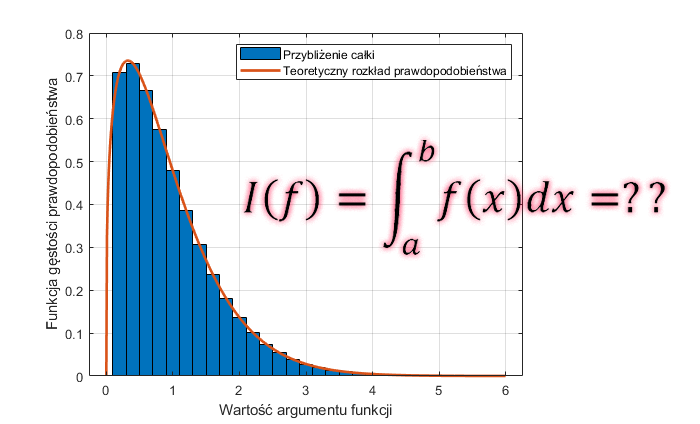
W fizyce i inżynierii często jedna wielkość jest wyrażana jako całka (oznaczona lub nieoznaczona) innej wielkości fizycznej. Dotyczy to szczególnie wszelkiego rodzaju przepływów i objętości. Na przykład strumień magnetyczny, dla dowolnej powierzchni przez którą przepływa, jest całką proporcjonalną do indukcji magnetycznej. Innym zagadnieniem, z którym często spotykamy się w praktyce jest obliczanie pola powierzchni pod fragmentem krzywej. Przykładem jest całkowanie funkcji gęstości prawdopodobieństwa, gdzie całka oznaczona w granicach od a do b jest miarą prawdopodobieństwa wystąpienia liczb z tego zakresu. Oczywiście całka oznaczona z takiej funkcji w granicach od minus do plus nieskończoności musi wynosić 1, czyli zdarzenie pewne. Wykorzystamy te cechę w przykładach poniżej.
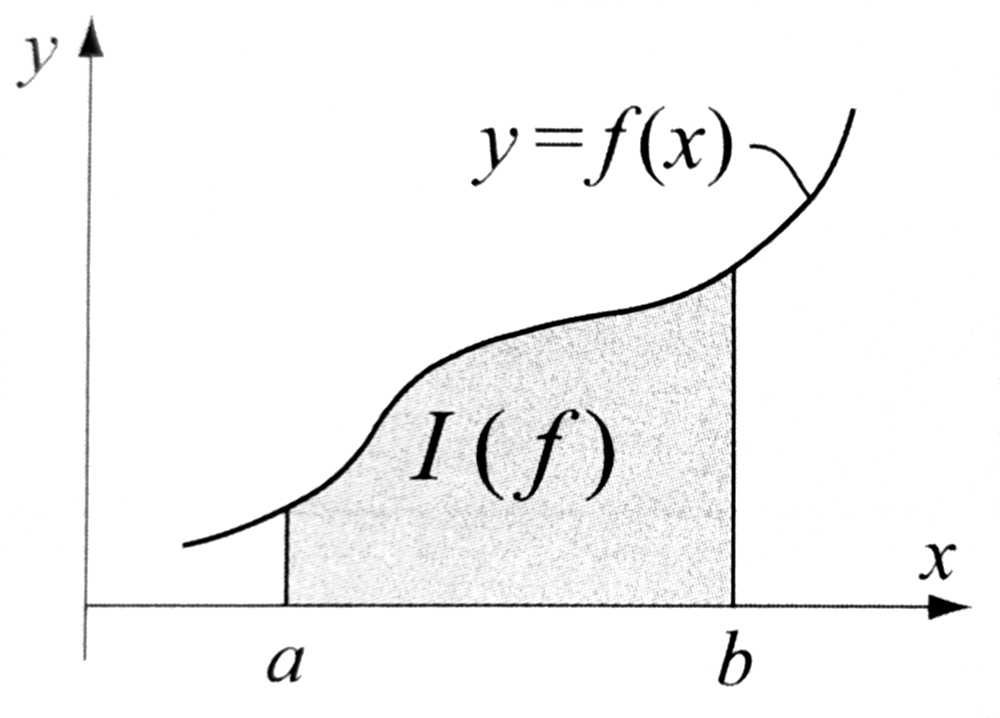
Całkę oznaczoną zdefiniujemy jako:

Gdzie: f(x) jest funkcją podcałkową niezależnego argumentu x, oraz a i b są granicami całkowania. Wartość całki jest liczbą jeżeli a i b są liczbami. Graficzna interpretacja całki jest pokazana na rysunku i odpowiada polu powierzchni pod krzywą w przedziale [a, b].
Analityczne obliczanie całki w MATLABie
Podobnie jak przy obliczaniu pochodnych, niektóre całki jesteśmy w stanie obliczyć analitycznie. Można to zrobić ręcznie, na kartce papieru, lub posłużyć się pakietem MATLAB i wykorzystać do tego celu Symbolic Math Toolbox. Sposób postępowania jest analogiczny jak przy różniczkowaniu, o czym pisałem w jednym z poprzednich wpisów. Jeżeli f, jest wyrażeniem symbolicznym, to użycie funkcji int(f), będzie skutkować próbą obliczenia całki w postaci symbolicznej. Zobaczmy kilka przykładów dla całek nieoznaczonych:
syms x; f = cos(x); int(f)
Jako wynik uzyskamy:
ans = sin(x)
Inny przykład wyrażenia arytmetycznego:
syms x; f = 3*x^2+4*x+1; int(f)
Jako wynik otrzymamy:
X^3+2x^2+x
Obydwa wyniki zgadzają się z teorią z dokładnością do stałej. Warto nadmienić, że funkcja int pozwala również obliczyć wartość całki dla danego argumentu, oraz całkę oznaczoną w przedziale. Sprawdźmy czy całka za okres funkcji sinus faktycznie wynosi 0:
syms x; int(sin(x), 0, 2*pi) % Wynik: ans = 0
Jeżeli nie zależy nam na obliczeniach symbolicznych, a jedynie obliczeniu wartości całki oznaczonej, można również użyć innej funkcji o podstawowej składni: I = integral(fun, xmin, xmax), gdzie fun to definicja funkcji, a xmin i xmax to granice całkowania.
fun = @(x) sin(x) integral(fun, 0, 2*pi) ans = -5.55e-17
Nie otrzymaliśmy dokładnego wyniku, chociaż wartość e-17 można uznać za zero „numeryczne”. Stało się tak dlatego, że funkcja integral realizuje numeryczne obliczanie całki, które jest jedynie przybliżeniem poprawnej wartości. Przyjrzyjmy się więc numerycznym metodom całkowania.
MATLAB całkowanie numeryczne
Podobnie jak miało to miejsce przy obliczaniu pochodnej, całkowanie numeryczne stosujemy wtedy, kiedy nie potrafimy obliczyć wartości całki w sposób analityczny bądź dysponujemy jedynie danymi pomiarowymi. Liczba metod całkowania jest duża, dlatego w tym miejscu skupię się na metodach najprostszych aby zobrazować idee całkowania numerycznego i pokazać jak to zrobić w programie MATLAB całkowanie numeryczne.
Metoda prostokątów
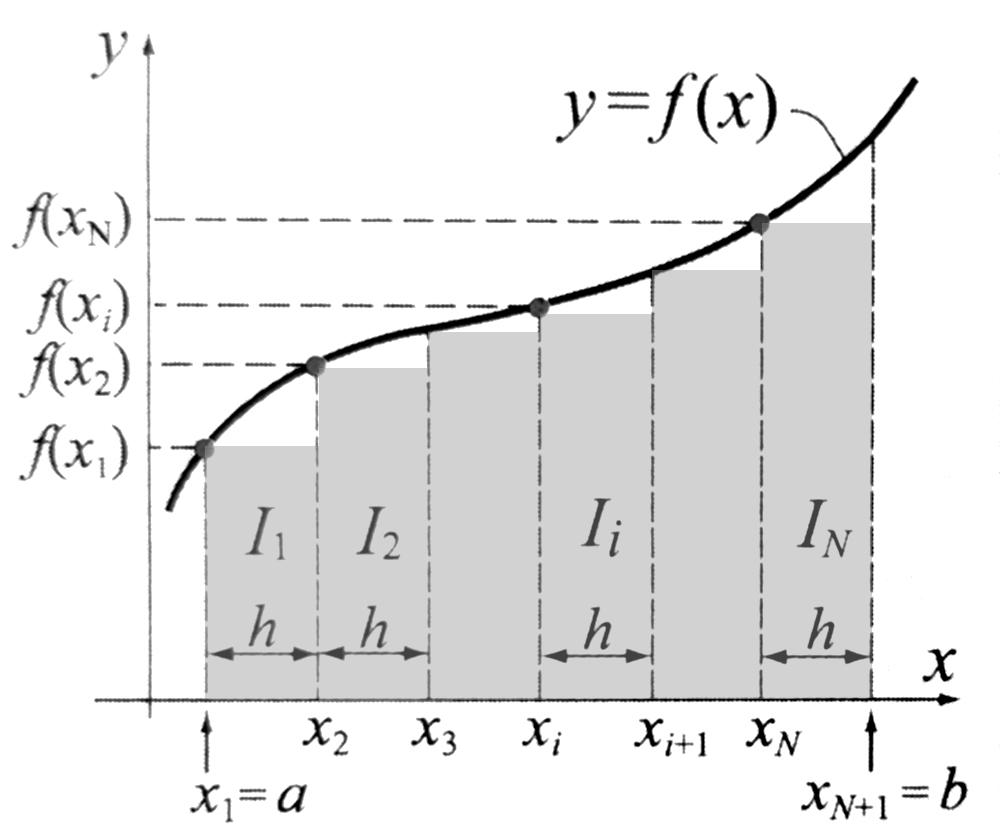
Jest to najprostsza metoda całkowania numerycznego lecz jednocześnie dająca duże błędy. Polega ona na przybliżeniu pola powierzchni pod f(x) w przedziale [a,b] sumą pól prostokątów, utworzonych przez podział [a,b] na N mniejszych podprzedziałów. Idea ta jest zobrazowana na rysunku, gdzie h to szerokość przedziału.

Przykład: Obliczyć całkę oznaczoną dla rozkładu prawdopodobieństwa Weilbull’a w zakresie [0,6]. Wiemy, że taka całka wynosi 1. Zatem odstępstwo od tej wartości będzie miarą błędu całkowania.
clear all; close all; clc
% Generacja wartości rozkładu prawdopodobieństwa
pd = makedist('Weibull',1,1.3);
% Rozkład "referencyjny" tylko na potrzeby rysunku (gęsto "próbkowany")
x_ref=0 : 0.01 : 6;
y_ref = pdf(pd,x_ref);
% Rozkład do całkowania z krokiem h
h = 0.2; % lub 0.1
x = 0 : h : 6;
y = pdf(pd,x);
% Całkowanie metodą prostokątów
I1 = h * sum (y)
figure; bar(x, y, 1);
hold on; plot(x_ref, y_ref, 'LineWidth', 2); grid on;
xlabel('Wartość argumentu funkcji'); ylabel('Funkcja gęstości prawdopodobieństwa');
legend('Przybliżenie całki', 'Teoretyczny rozkład prawdopodobieństwa');
Dla szerokości przedziału h = 0.2, wartość całki wyniosła 0.95 (błąd 5%), a dla h = 0.1 całka ma wartość 0.98 (błąd 2%). Im mniejszy przedział całkowania, tym dokładniejsze obliczenia (prostokąty „szczelniej” wypełniają pole pod krzywą).
Metoda punktów środkowych
Modyfikacją metody prostokątów jest metoda punktów środkowych. Tutaj również oblicza się pole powierzchni danego przedziału, jednak do obliczeń należy wziąć wartość środkową argumentu. Ilustruje to rysunek.

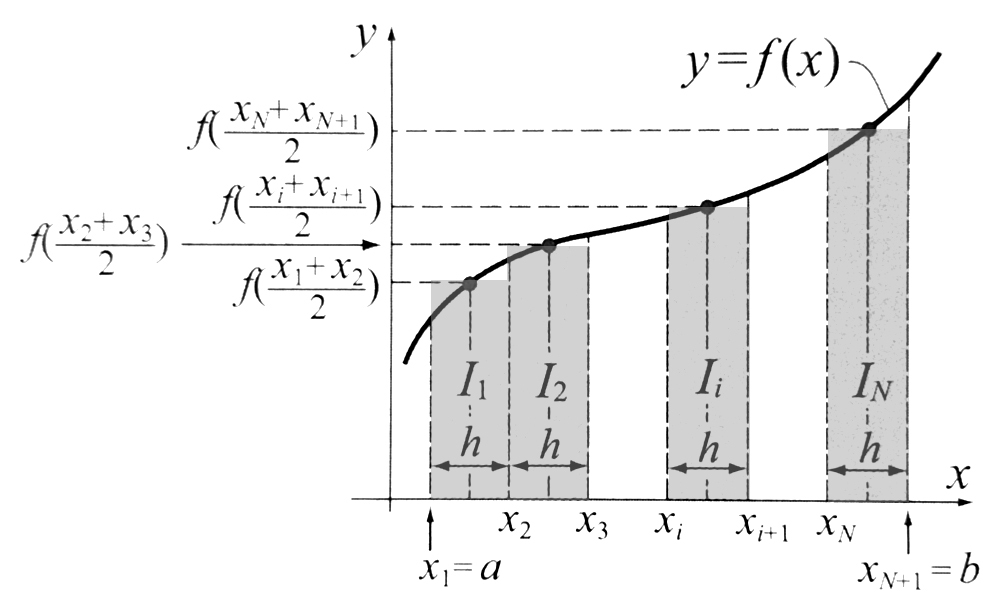
Dzięki takiemu podejściu metoda ta, szczególnie dla przebiegów monotonicznych jest dokładniejsza niż metoda prostokątów, gdzie do całkowania jest brana wartość dla skrajnej wartości argumentu.
Przykład: obliczmy całkę metodą punktów środkowych dla poprzedniego przykładu i rozkładu Weilbull’a.
clear all; close all; clc
% Generacja wartości rozkładu prawdopodobieństwa
pd = makedist('Weibull',1,1.3);
% Rozkład "referencyjny" tylko na potrzeby rysunku (gęsto "próbkowany")
x_ref=0 : 0.01 : 6;
y_ref = pdf(pd,x_ref);
% Rozkład do całkowania z krokiem h
h = 0.2; % lub 0.1
x = 0 : h : 6;
y = pdf(pd,x);
% Całkowanie metodą punktów środkowych
x_central = (x(1:end-1) + x(2:end))/2;
y_central = pdf(pd,x_central);
I2 = h * sum (y_central)
figure; bar(x, y, 1);
hold on; plot(x_ref, y_ref, 'LineWidth', 2); grid on;
xlabel('Wartość argumentu funkcji'); ylabel('Funkcja gęstości prawdopodobieństwa');
legend('Przybliżenie całki', 'Teoretyczny rozkład prawdopodobieństwa');
Pamiętamy, że dokładna wartość takiej całki wynosi 1. Dla metody punktów środkowych otrzymujemy: dla szerokości przedziału h = 0.2, wartość całki wynosi 1.0086 (błąd 0.856%), a dla h = 0.1 całka ma wartość 1.0035 (błąd 0.351%). Jak widać w obydwu przypadkach błędy całkowania są dużo mniejsze niż dla klasycznej metody prostokątów.
Metoda trapezów
W metodzie trapezów obliczane jest dodatkowe pole pod krzywą, dzięki czemu otrzymujemy dokładniejsze przybliżenie całki. Metoda ta jest zilustrowana na rysunku.

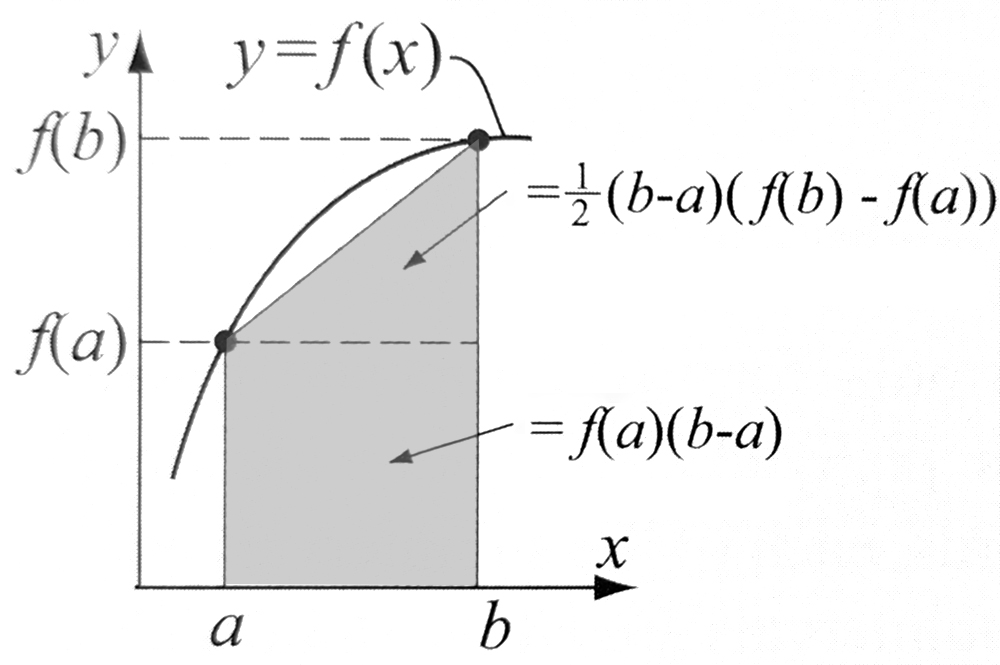
W MATLABie metoda trapezów jest zaimplementowana we funkcji trapz.
Czyli jak całkować w MATLABie?
MATLAB całkowanie numeryczne - czyli jak to się robi dzisiaj? Na przestrzeni lat rozwinięto i udoskonalono wiele innych, bardziej dokładnych metod całkowania niż te opisane powyżej. Polegają one na przybliżeniu funkcji podcałkowej lub jej fragmentów za pomocą innej funkcji, dla której wartość całki jest dokładnie znana. W zależności od algorytmu całkowania i wyboru tzw. węzłów całkowania rozróżnia się metody Newtona – Cotesa, Simpsona lub Gaussa. O szczegółach tych metod można przeczytać w literaturze tematu. Podsumowując:
- Jeżeli chcemy analitycznie obliczyć całkę nieoznaczoną to można to zrobić symbolicznie za pomocą funkcji int.
- Jeżeli dysponujemy opisem analitycznym funkcji podcałkowej, ale chcemy policzyć wartość całki oznaczonej to to robimy to za pomocą funkcji integral.
- Dla danych pomiarowych, dla których nie mamy opisu analitycznego, całkowanie można wykonać metodą trapezów, bądź punktów centralnych.
Bibliografia: A. Gilat, V. Subramaniam, "Numerical Methods", Wiley, 2011.