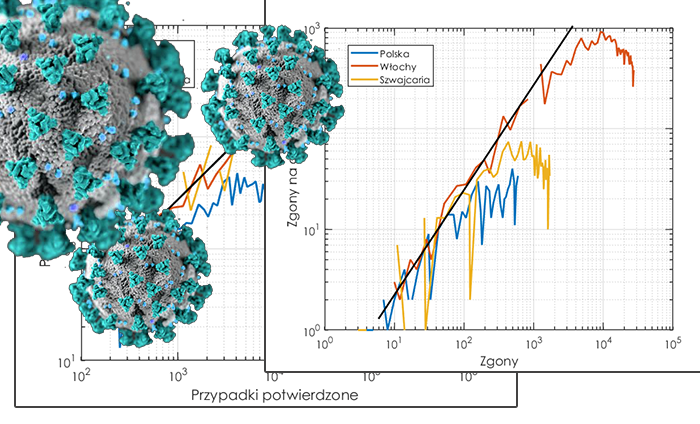
Tym razem zajmiemy się lepszym zobrazowaniem dynamiki rozwoju pandemii oraz „unormujemy” czas na wykresach, dzięki czemu będzie można odpowiedzieć na pytanie: „co by było gdyby choroba zaczęła się rozwijać w różnych krajach w tym samym momencie?”

Po poprzednim wpisie dotarły do mnie uwagi, że zaprezentowane wykresy nie do końca wiarygodnie obrazują stan rozprzestrzeniania się pandemii oraz liczność nowych zakażeń, wyzdrowień i zgonów. Głównym argumentem była niewiarygodność danych, a szczególnie mała liczba przeprowadzanych testów na obecność wirusa w danym kraju.

Cóż, wyniki analizy są tak wiarygodne, jak dostarczone dane.  W niczym nie ujmuje to przyjętej metodologii badawczej. Dlatego na programy prezentowane w postach, które dotyczą problemu pandemii należy patrzeć się od strony programowo/obliczeniowej.

Wróćmy jednak do naszego programu. W poprzednim poście skupiłem się na dynamice wskaźników związanych z obecnością wirusa. Jednak rysowanie wykresów w funkcji czasu, jakkolwiek daje pewien obraz sytuacji, to utrudnia analizę. Po pierwsze dlatego, że w różnych krajach początek zakażeń miał miejsce w różnym czasie, a po drugie dlatego, że na podstawie analizy wykresów w funkcji czasu trudno jest oszacować ogólny trend.  

Mimo tego, spróbujmy „wyrównać” czas wystąpienia wirusa w różnych krajach do tej samej chwili czasu. To pozwoli na bezpośrednie porównanie dynamiki wzrostu wskaźników, bez względu na czas wystąpienia choroby. Załóżmy więc, że poziomem odniesienia jest co najmniej 100 stwierdzonych przypadków koronawirusa w danym kraju, i wyrównajmy wykresy względem tej chwili czasu:

[Indx_Poland]  = find(Poland_confirmed{:,5:end}>100);


Poland_confirmed(:,5:end) = array2table([Poland_confirmed{:, (5+Indx_Poland(1)):end} nan(1,Indx_Poland(1))]);
Poland_deaths(:,5:end) = array2table([Poland_deaths{:, (5+Indx_Poland(1)):end} nan(1,Indx_Poland(1))]);
Poland_recovered(:,5:end) = array2table([Poland_recovered{:, (5+Indx_Poland(1)):end} nan(1,Indx_Poland(1))]);

Poniższe rysunki obrazują liczbę osób zarażonych i zgonów w sytuacji gdyby choroba rozpoczęła się we wszystkich krajach w tym samym dniu 22 stycznia.

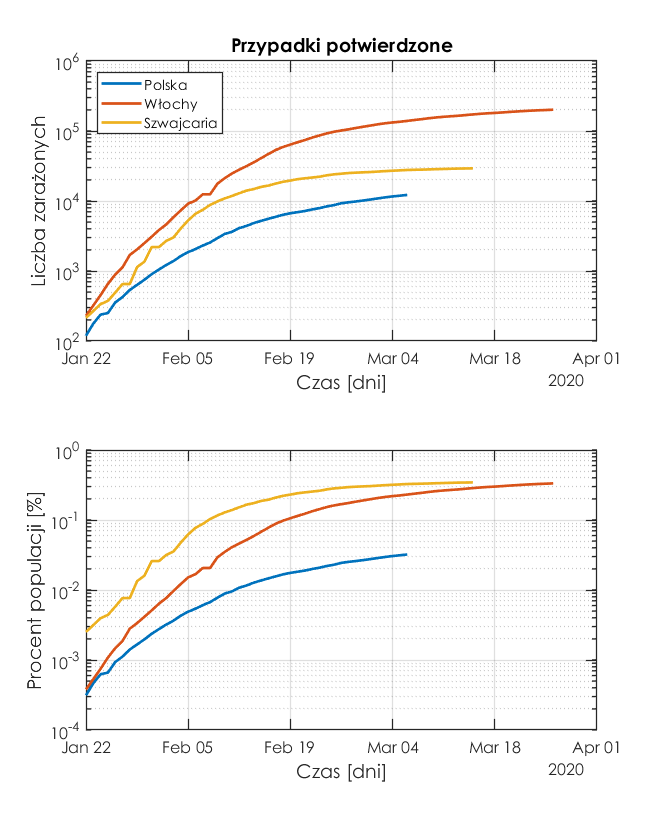
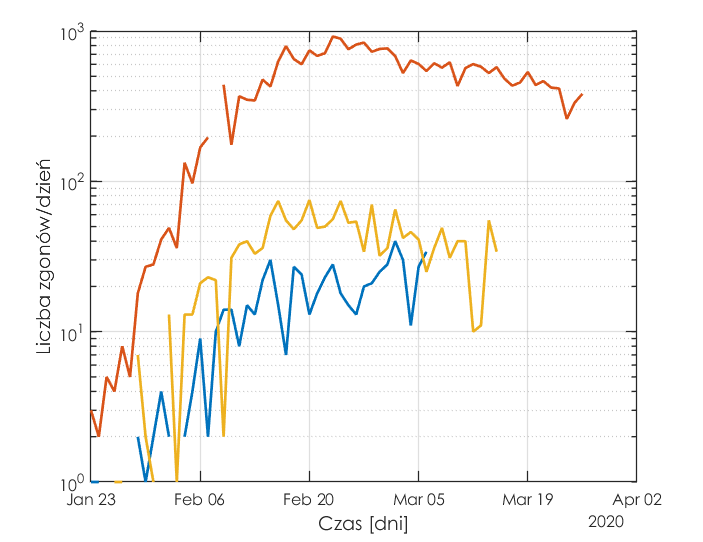
Obrazowanie dynamiki wzrostu w funkcji czasu, nawet jeśli unormujemy czas wystąpienia danego poziomu zakażeń na wykresach nie jest najlepszym pomysłem. Istotna jest liczba nowych zakażeń w stosunku do stwierdzonych zakażeń. Ta względna liczba daje obraz dynamiki przyrostu (lub zmniejszania się) liczby osób chorych. Podsumowując, program z poprzedniego postu, można ulepszyć w następujący sposób:

Używamy wyłącznie skali logarytmicznej na obydwu osiach – pozwala to na lepsze zobrazowanie różnic pomiędzy krajami o skrajnie różnej liczbie przypadków dotkniętych COVID-19. Małe liczby są „skalowane” do góry, a duże lepiej „obrazowane” na tle liczb małych. W tej skali przyrost wykładniczy ma charakter prostej.

Analizujemy przyrosty liczby chorych/wyleczonych/zgonów zamiast wartości bezwzględnych przypadków – umożliwia to lepiej zobrazować trend i sprawdzić czy liczba osób chorych ma tendencję wzrostową czy malejącą.

Czas nie ma znaczenia – dynamika wzrostu liczby osób zakażonych nie zależy wprost od czasu (czy to jest styczeń czy luty) ale warunków środowiskowych, społecznych, stopnia ochrony społeczeństwa, itp. Dlatego  zamiast rysować wykres w funkcji czasu lepiej jest narysować przyrost liczby nowych przypadków w funkcji wszystkich stwierdzonych przypadków. To swego rodzaju normowanie daje lepszy obraz dynamiki rozwoju pandemii.

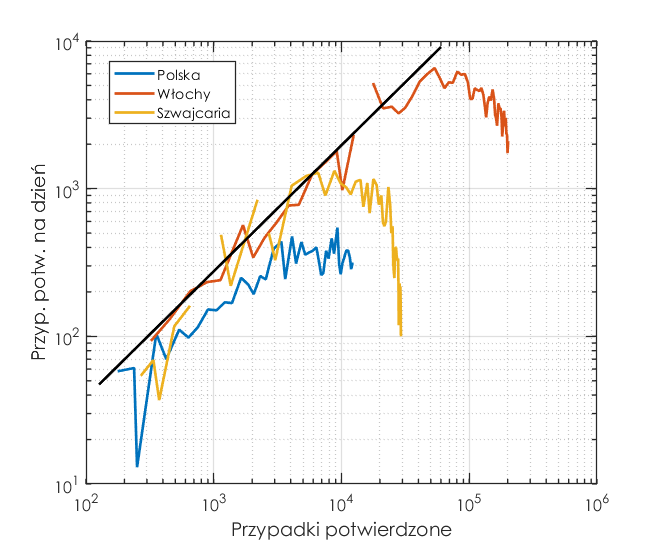
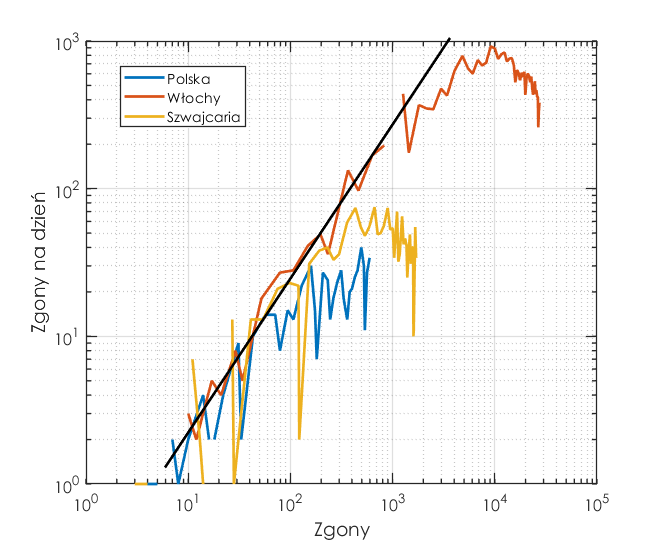
Na rysunkach czarna linia prosta reprezentuje trend o stałej liczbie przyrostu chorych/zgonów. Wynika to wprost z modelu wykładniczego, który opisuje dynamikę rozprzestrzeniania się wirusa. W skali logarytmicznej przyrosty wykładnicze o takim samym tempie wzrostu reprezentuje prosta. A zatem dla danych z różnych krajów odstępstwo trendu powyżej tej linii oznacza wzrost liczby przypadków, a poniżej tej linii oznacza, że choroba wyhamowuje. Dla Włoch i Szwajcarii widać wyraźnie spadek liczby nowych osób chorych oraz zgonów. W Polsce ten trend dopiero się zaczyna. Bądźmy dobrej myśli!

Poniżej znajduje się cały zmodyfikowany program.

clear all; close all; clc

% Program na podstawie skryptu E. Cheynet'a i funkcji:
% [tableConfirmed,tableDeaths,tableRecovered,time] = getDataCOVID()
% Program pobiera dane dotyczące liczby zachorowań na COVID-19 z bazy
% danych uniwersytetu John'a Hopkins'a oraz wykonuje prostą analizę danych.
% 
% Referencje:
% [1] https://github.com/CSSEGISandData/COVID-19


%% Parametry importu danych

% Liczba dni do analizy od początku rejestracji danych
Ndays = floor(datenum(now))-datenum(2020,01,22)-1; % minus jeden dzień bo baza danych jest odświeżana co 24h

% Ustawienie parametrów importu danych
opts = delimitedTextImportOptions("NumVariables", Ndays+5);

% Dzięki użyciu tabeli, każdej zmiennej można nadać nazwę symboliczną 
% i się nią posługiwać w programie
opts.VariableNames = ["ProvinceState", "CountryRegion", "Lat", "Long", repmat("data",1,Ndays+1)];

% Definicja typu każdej zmiennej, dwie pierwsze to stringi, reszta wartości numeryczne: 
opts.VariableTypes = ["string", "string", repmat("double",1,Ndays+3)];

% Pozostałe ustawienia importu danych
opts.ExtraColumnsRule = "ignore";   % w przypadku występowania dodatkowych kolumn - ignorujemy je
opts.EmptyLineRule = "read";        % jeżeli w danych występują puste linie to je odczytujemy

%% Import danych

% Dane podzielone na trzy grupy: zarażeni, zgony i wyleczenia
status = {'confirmed','deaths','recovered'};

% Adres repozytorium Uniwersytetu John'a Hopkins'a
address = 'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/';
ext = '.csv';

% Odczyt danych 
for ii = 1:numel(status)
    
    filename = ['time_series_covid19_',status{ii},'_global'];
    fullName = [address,filename,ext];
    urlwrite(fullName,'dummy.csv');     % import danych do pliku, którego zawartość
    % będzie następnie konwertowana na tabelę:
        
    if strcmpi(status{ii},'Confirmed')
        tableConfirmed =readtable('dummy.csv', opts);
        
    elseif strcmpi(status{ii},'Deaths')
        tableDeaths =readtable('dummy.csv', opts);
        
    elseif strcmpi(status{ii},'Recovered')
        tableRecovered =readtable('dummy.csv', opts);
    else
        error('Unknown status')
    end
end

% Odczyt daty i jej konwersja na postać standardową
fid = fopen('dummy.csv');
time = textscan(fid,repmat('%s',1,size(tableRecovered,2)), 1, 'Delimiter',',');
time(1:4)=[];
time = datetime([time{1:end}])+years(2000);
fclose(fid);

% delete('dummy.csv'); % plik można skasować lub zostawić (przydatne przy
% braku połączenia z Internetem


%% Analiza danych 

% Dane dla Polski
Poland_population = 38*10^6;
Poland_confirmed = tableConfirmed(tableConfirmed.CountryRegion == 'Poland',:);
Poland_deaths = tableDeaths(tableConfirmed.CountryRegion == 'Poland',:);
Poland_recovered = tableRecovered(tableConfirmed.CountryRegion == 'Poland',:);

% Normowanie czasu 
[Indx_Poland]  = find(Poland_confirmed{:,5:end}>100);
Poland_confirmed(:,5:end) = array2table([Poland_confirmed{:, (5+Indx_Poland(1)):end} nan(1,Indx_Poland(1))]);
Poland_deaths(:,5:end) = array2table([Poland_deaths{:, (5+Indx_Poland(1)):end} nan(1,Indx_Poland(1))]);
Poland_recovered(:,5:end) = array2table([Poland_recovered{:, (5+Indx_Poland(1)):end} nan(1,Indx_Poland(1))]);

% Procent zachorowań w stosunku do liczby mieszkańców
Poland_conf_ratio = 100*Poland_confirmed{:,5:end}/Poland_population;
Poland_deaths_ratio = 100*Poland_deaths{:,5:end}/Poland_population;
Poland_recovered_ratio = 100*Poland_recovered{:,5:end}/Poland_population;
% Śmiertelność
Poland_mortality_ratio = 100*Poland_deaths{:,5:end}./(Poland_recovered{:,5:end}+Poland_confirmed{:,5:end});

% Dane dla kraju nr 1
Country1 = 'Italy'
Country1_population = 60.4*10^6;
Country1_confirmed = tableConfirmed(tableConfirmed.CountryRegion == Country1,:);
Country1_deaths = tableDeaths(tableConfirmed.CountryRegion == Country1,:);
Country1_recovered = tableRecovered(tableConfirmed.CountryRegion == Country1,:);

% Normowanie czasu
[Indx_Country1]  = find(Country1_confirmed{:,5:end}>100);
Country1_confirmed(:,5:end) = array2table([Country1_confirmed{:, (5+Indx_Country1(1)):end} nan(1,Indx_Country1(1))]);
Country1_deaths(:,5:end) = array2table([Country1_deaths{:, (5+Indx_Country1(1)):end} nan(1,Indx_Country1(1))]);
Country1_recovered(:,5:end) = array2table([Country1_recovered{:, (5+Indx_Country1(1)):end} nan(1,Indx_Country1(1))]);

% Procent zachorowań w stosunku do liczby mieszkańców
Country1_conf_ratio = 100*Country1_confirmed{:,5:end} / Country1_population; 
Country1_deaths_ratio = 100*Country1_deaths{:,5:end} / Country1_population; 
Country1_recovered_ratio = 100*Country1_recovered{:,5:end} / Country1_population; 
% Śmiertelność
Country1_mortality_ratio = 100*Country1_deaths{:,5:end}./(Country1_recovered{:,5:end}+Country1_confirmed{:,5:end});

% Dane dla kraju nr 2
Country2 = 'Switzerland'
Country2_population = 8.5*10^6;
Country2_confirmed = tableConfirmed(tableConfirmed.CountryRegion == Country2,:);
Country2_deaths = tableDeaths(tableConfirmed.CountryRegion == Country2,:);
Country2_recovered = tableRecovered(tableConfirmed.CountryRegion == Country2,:);

% Normowanie czasu
[Indx_Country2]  = find(Country2_confirmed{:,5:end}>100);
Country2_confirmed(:,5:end) = array2table([Country2_confirmed{:, (5+Indx_Country2(1)):end} nan(1,Indx_Country2(1))]);
Country2_deaths(:,5:end) = array2table([Country2_deaths{:, (5+Indx_Country2(1)):end} nan(1,Indx_Country2(1))]);
Country2_recovered(:,5:end) = array2table([Country2_recovered{:, (5+Indx_Country2(1)):end} nan(1,Indx_Country2(1))]);

% Procent zachorowań w stosunku do liczby mieszkańców
Country2_conf_ratio = 100*Country2_confirmed{:,5:end} / Country2_population; 
Country2_deaths_ratio = 100*Country2_deaths{:,5:end} / Country2_population; 
Country2_recovered_ratio = 100*Country2_recovered{:,5:end} / Country2_population; 
% Śmiertelność
Country2_mortality_ratio = 100*Country2_deaths{:,5:end}./(Country2_recovered{:,5:end}+Country2_confirmed{:,5:end});


% Tempo przyrostu zakażeń
delta_Poland = diff(Poland_confirmed{1,5:end});
delta_Country1 = diff(Country1_confirmed{1,5:end});
delta_Country2 = diff(Country2_confirmed{1,5:end});

% Tempo przyrostu zgonów
delta_deaths_Poland = diff(Poland_deaths{1,5:end});
delta_deaths_Country1 = diff(Country1_deaths{1,5:end});
delta_deaths_Country2 = diff(Country2_deaths{1,5:end});


%% Rysunki

% Polska w skali liniowej
figure; subplot(211); plot(time, Poland_confirmed{:,5:end}, time, Poland_deaths{:,5:end}, time, Poland_recovered{:,5:end})
my_figure('Czas [dni]', 'Liczba osób', 'Polska'); grid on;
legend('Zarażeni','Zgony','Wyzdrowienia','Location','northwest')

subplot(212); semilogy(time, Poland_conf_ratio, time, Poland_deaths_ratio, time, Poland_recovered_ratio)
my_figure('Czas [dni]', 'Procent populacji [%]', ' '); grid on;

% Polska w skali logarytmicznej
figure; subplot(211); semilogy(time, Poland_confirmed{:,5:end}, time, Poland_deaths{:,5:end}, time, Poland_recovered{:,5:end})
my_figure('Czas [dni]', 'Liczba osób', 'Polska'); grid on;
legend('Zarażeni','Zgony','Wyzdrowienia','Location','northwest')

subplot(212); semilogy(time, Poland_conf_ratio, time, Poland_deaths_ratio, time, Poland_recovered_ratio)
my_figure('Czas [dni]', 'Procent populacji [%]', ' '); grid on;

% Zarażeni w skali liniowej
figure; subplot(211); plot(time, Poland_confirmed{:,5:end}, time, Country1_confirmed{:,5:end}, time, Country2_confirmed{:,5:end})
my_figure('Czas [dni]', 'Liczba zarażonych', 'Przypadki potwierdzone'); grid on;
legend('Polska','Włochy','Szwajcaria','Location','northwest')

subplot(212); plot(time, Poland_conf_ratio, time, Country1_conf_ratio, time, Country2_conf_ratio)
my_figure('Czas [dni]', 'Procent populacji [%]', ' '); grid on;

% Zarażeni w skali logarytmicznej
figure; subplot(211); semilogy(time, Poland_confirmed{:,5:end}, time, Country1_confirmed{:,5:end}, time, Country2_confirmed{:,5:end})
my_figure('Czas [dni]', 'Liczba zarażonych', 'Przypadki potwierdzone'); grid on;
legend('Polska','Włochy','Szwajcaria','Location','northwest')

subplot(212); semilogy(time, Poland_conf_ratio, time, Country1_conf_ratio, time, Country2_conf_ratio)
my_figure('Czas [dni]', 'Procent populacji [%]', ' '); grid on;

% Szybkość zakażeń
figure; subplot(211); plot(time(2:end), delta_Poland, time(2:end), delta_Country1, time(2:end), delta_Country2)
my_figure('Czas [dni]', 'Liczba zarażonych/dzień', 'Przypadki potwierdzone - tempo wzrostu na dzień'); grid on;
legend('Polska','Włochy','Szwajcaria','Location','northwest')

subplot(212); semilogy(time(2:end), delta_Poland, time(2:end), delta_Country1, time(2:end), delta_Country2)
my_figure('Czas [dni]', 'Liczba zarażonych/dzień', ' '); grid on;

% Zgony w skali logarytmicznej
figure; subplot(211); semilogy(time, Poland_deaths{:,5:end}, time, Country1_deaths{:,5:end}, time, Country2_deaths{:,5:end})
my_figure('Czas [dni]', 'Liczba zgonów', 'Zgony'); grid on;
legend('Polska','Włochy','Szwajcaria','Location','northwest')

subplot(212); semilogy(time, Poland_deaths_ratio, time, Country1_deaths_ratio, time, Country2_deaths_ratio)
my_figure('Czas [dni]', 'Procent populacji [%]', ' '); grid on;

% Szybkość zgonów
figure; subplot(211); plot(time(2:end), delta_deaths_Poland, time(2:end), delta_deaths_Country1, time(2:end), delta_deaths_Country2)
my_figure('Czas [dni]', 'Liczba zgonów/dzień', 'Zgony - tempo wzrostu na dzień'); grid on;
legend('Polska','Włochy','Szwajcaria','Location','northwest')

subplot(212); semilogy(time(2:end), delta_deaths_Poland, time(2:end), delta_deaths_Country1, time(2:end), delta_deaths_Country2)
my_figure('Czas [dni]', 'Liczba zgonów/dzień', ' '); grid on;

% Śmiertelność w skali logarytmicznej
figure;  plot(time, Poland_mortality_ratio, time, Country1_mortality_ratio, time, Country2_mortality_ratio)
my_figure('Czas [dni]', 'Śmiertelność [%]', 'Śmiertelność'); grid on;
legend('Polska','Włochy','Szwajcaria','Location','northwest')

% Wyzdrowieni w skali logarytmicznej
figure; subplot(211); semilogy(time, Poland_recovered{:,5:end}, time, Country1_recovered{:,5:end}, time, Country2_recovered{:,5:end})
my_figure('Czas [dni]', 'Liczba wyzdrowiałych', 'Wyzdrowienia'); grid on;
legend('Polska','Włochy','Szwajcaria','Location','northwest')

subplot(212); semilogy(time, Poland_recovered_ratio, time, Country1_recovered_ratio, time, Country2_recovered_ratio)
my_figure('Czas [dni]', 'Procent populacji [%]', ' '); grid on;


%% Nowe rysunki

% Przypadki potwierdzone
figure; loglog(Poland_confirmed{:,6:end}, delta_Poland, Country1_confirmed{:,6:end}, delta_Country1, Country2_confirmed{:,6:end}, delta_Country2)
my_figure('Przypadki potwierdzone', 'Przyp. potw. na dzień', '--'); grid on;
legend('Polska','Włochy', 'Szwajcaria', 'northwest')

% Zgony
figure; loglog(Poland_deaths{:,6:end}, delta_deaths_Poland, Country1_deaths{:,6:end}, delta_deaths_Country1, Country2_deaths{:,6:end}, delta_deaths_Country2)
my_figure('Zgony', 'Zgony na dzień', '--'); grid on;
legend('Polska','Włochy', 'Szwajcaria', 'northwest')



function my_figure(opisX, opisY, tytul)
%% Zmienione argumenty wejściowe funkcji na opisy osi!

%% CREATEFIGURE2(X1, Y1) <-- Taka była pierwotna składnia funkcji.
%  X1:  vector of x data
%  Y1:  vector of y data

%  Auto-generated by MATLAB on 18-Mar-2020 10:38:53

% Create figure
% figure1 = figure; % To usuwamy, gdyż rysunek będzie tworzony 
                    % na zewnątrz funkcji

% Create axes
% axes1 = axes;     % To również usuwamy, gdyż obiekt axes, jest już
                    % stworzony na aktywnym rysunku
axes1 = gca;
hold(axes1,'on');

r = groot;
monitors = r.MonitorPositions;
figure1 = gcf; 
figure1.Position = [monitors(1,1)+200 monitors(2,4)/5 660 820];

% Create plot
% plot(X1,Y1,'LineWidth',2);    % To samo dotyczy linii

% Create ylabel
% ylabel({'Opis osi Y'});       % Podmieniamy, tak aby móc wprowadzać
ylabel(opisY);                  % swój tekst. Podobnie z xlabel i title

% Create xlabel
xlabel(opisX);

% Create title
title(tytul);

% Uncomment the following line to preserve the X-limits of the axes
% xlim(axes1,[0 1]);
box(axes1,'on');
% Set the remaining axes properties
set(axes1,'FontName','Century Gothic','FontSize',12,...
    'LabelFontSizeMultiplier',1.2,'TitleFontSizeMultiplier',1.2,'XGrid','on',...
    'LineWidth',1,'TickLength',[0.02 0.025],'XMinorTick','on','YGrid','on','YMinorTick','on');

%% Jeżeli rysunek zawiera więcej niż jedną linia, konieczna jest pętla:

liczba_lini = size(axes1.Children);
for k = 1 : liczba_lini
    axes1.Children(k,1).LineWidth = 2;
end

end