Jakiś czas temu na naszym blogu opublikowałem serię wpisów na temat (dyskretnej) transformaty Fouriera – DFT (część 1, część 2, część 3). Omawiałem w nich cechy i właściwości tego narzędzia do analizy częstotliwościowej sygnałów, a domknięciem był film na temat konsekwencji próbkowania sygnałów.
Bieżący wpis w dużej mierze bazuje na tamtej serii artykułów i dotyczy metod czasowo – częstotliwościowej analizy sygnałów. Metody te, w pewnym sensie, są rozszerzeniem klasycznej transformaty Fouriera na obszar sygnałów niestacjonarnych. Co to oznacza?
Sygnały stacjonarne i niestacjonarne
Jednym z kryteriów podziału sygnałów jest cecha stacjonarności. Bez wchodzenia w matematyczne szczegóły, można powiedzieć, że sygnał stacjonarny to taki, który nie zmienia swoich parametrów w czasie. Przykładem sygnału stacjonarnego jest sinus o stałej częstotliwości i amplitudzie, szum biały o stałej wartości średniej i odchyleniu standardowym, itd. Na poniższym rysunku przedstawiono przykłady takich sygnałów oraz ich widma.

Jak widać widmo sygnałów stacjonarnych obliczone za pomocą DFT dobrze obrazuje ich strukturę częstotliwościową. DFT jest stworzone do analizy takich sygnałów.
Jeżeli jednak w czasie obserwacji sygnał zmienia swoje parametry, to mówimy, że jest niestacjonarny. Przykładem jest sinus o zmiennej częstotliwości i/lub amplitudzie, albo szum biały, w którym zmienia się wartość średnia:

W przypadku sygnałów niestacjonarnych, użycie DFT daje nam dziwny obraz widma. Jest ono jakby rozmyte. Wydaje się, że do ich analizy należy używać innych narzędzi.
W życiu codziennym wiele rejestrowanych przez nas sygnałów jest niestacjonarnych – niestacjonarność jest niejako wrodzoną cechą zjawisk, które są źródłem obserwowanych sygnałów: mowa ludzka, oscylacje w układach elektrycznych, wibracje elementów maszyn i pojazdów, drgania gruntu czy sygnały medyczne. Na rysunku przedstawiono niestacjonarny sygnał mowy ludzkiej (słowo metrologia):

Do analizy widmowej i przetwarzania sygnałów niestacjonarnych używa się metod czasowo – częstotliwościowych.
Czasowo – częstotliwościowa analiza sygnałów
Metody czasowo częstotliwościowej analizy sygnałów, umożliwiają, między innymi, zobrazowanie zmienności amplitudy, częstotliwości i fazy sygnału w czasie jego obserwacji. Innymi słowy widmo sygnału jest wyznaczane w czasie, co umożliwia „śledzenie” zmian struktury częstotliwościowej analizowanego sygnału. Porównajmy widma sygnału mowy ludzkiej dla słowa metrologia. Częstotliwość próbkowania wynosiła 44100Hz. Po lewej stronie jest widmo obliczone za pomocą tradycyjnego DFT, a po prawej wynik analizy czasowo – częstotliwościowej.


Zwróćcie uwagę na opis osi drugiego rysunku: oś y – częstotliwość, oś x – czas, a amplituda jest zobrazowana poprzez kolor. Mamy więc obraz chwilowych zmian częstotliwości (i amplitudy) w funkcji czasu (obserwacji sygnału)!
Widzimy, że dla badanego sygnału mowy częstotliwość zmienia się w czasie w zależności od wypowiadanych głosek. Takiego wniosku nie dałoby się wyciągnąć na podstawie klasycznej analizy DFT!
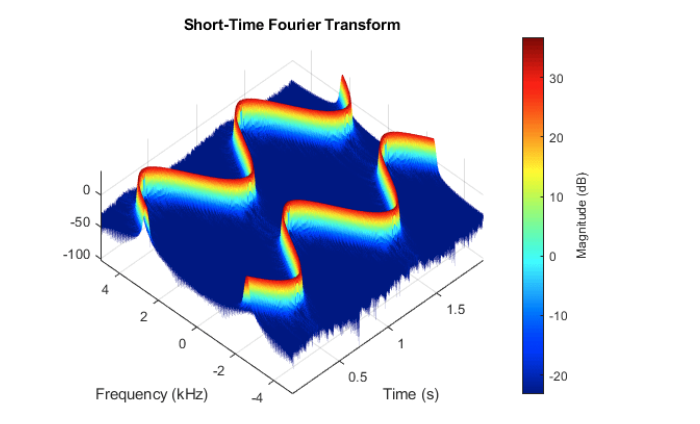
Weźmy kolejny przykład. Syntetyczny sygnał wygenerowany w MATLABie – sinus o zmieniającej się częstotliwości o 0.1 do 0.4kHz. Poniższy rysunek obrazuje sygnał i jego widmo dla częstotliwości próbkowania 5kHz. Dla czytelności przedstawiono wycinek z pełnego rysunku w zakresie czasu 0.3 – 1.4 sekundy i dla częstotliwości 0 – 1 kHz.


Ponownie, jedynie czasowo – częstotliwościowa analiza sygnałów umożliwia nam wgląd w to co dzieje się z sygnałem niestacjonarnym. W tym przypadku wyraźnie widać, jak zmienia się częstotliwość sygnału w czasie- coś co było poza zasięgiem klasycznej DFT.
Od strony matematycznej czasowo – częstotliwościowa analiza sygnałów jest zagadnieniem złożonym. Nie chce tu więc pisać o funkcjach bazowych, ortogonalnych i innych zawiłościach przetwarzania sygnałów. Warto jednak wspomnieć o takich formalizmach jak transformacja Gabora, krótkoczasowa transformacja Fouriera czy transformacja falkowa.
Krótkoczasowa transformacja Fouriera
Jednym z narzędzi czasowo – częstotliwościowej analizy sygnałów, które umożliwia wyznaczenie zmian widma sygnału w czasie jest krótkoczasowa transformacja Fouriera. Idea polega tutaj na przesuwającym się wzdłuż sygnału oknie czasowym, które z całego sygnału, „wycina” jego mniejsze fragmenty, poddawane następnie przekształceniu Fouriera.
Idee metody dobrze obrazuje poniższy rysunek. Sygnał ma długość N próbek, a okno czasowe (tutaj trójkątne) długość M. Okno przesuwa się „wzdłuż” sygnału co R próbek, przy czym najczęściej R < M, a więc jest stosowane nachodzenie okien na siebie, czyli tzw. overlaping.
Dla każdego fragmentu wyciętego przez tak przesuwające się okno jest obliczana DTF.

MATLAB a czasowo – częstotliwościowa analiza sygnałów
MATLAB oferuje szereg funkcji do czasowo – częstotliwościowej analizy sygnałów. Krótkoczasowa transformacja Fouriera jest zaimplementowana we funkcji stft, ale to tylko jedno z narzędzi dostępnych w pakiecie Mathworks’a. Zachęcam was do eksploracji tematu na własną rękę. Wystarczy wpisać w helpie „Time-Frequency Analysis”, a temat nie będzie miał dla Was tajemnic.