Metoda najmniejszej sumy kwadratów (LS - Least Squares) jest powszechnie wykorzystywana do aproksymacji danych pomiarowych modelami różnych rzędów. Tak jest również w przypadku MATLABa i oferowanych przez curve fitting toolbox funkcji. W tym wpisie zajmę się wytłumaczeniem na czym ta metoda polega oraz jakie są jej cechy. Pozwoli to Wam świadomie wykonywać aproksymacje danych bez często popełnianych przez użytkowników błędów.

Wstęp

Klasyczny problem z jakim często się spotykamy polega na dopasowaniu modelu w postaci równania prostej do danych pomiarowych.

Weźmy na przykład taką sytuacje, gdzie mamy zbiór wartości zmiennej niezależnej u i wartości y:

W szkole średniej lub na studiach nauczono nas, że liniową aproksymacje danych wykonujemy za pomocą powyższej prostej, której współczynniki obliczamy na podstawie poniższych wzorów:

gdzie:

ui – i-ta wartość zmiennej niezależnej,

yi – i-ta wartość rzędnej, odpowiadająca wartości ui,

N – liczba punktów pomiarowych.

Można przyjąć za pewnik, że tak po prostu jest i zastosować powyższe wzory. Spróbujmy jednak iść o krok dalej i zastanowić się skąd wzięły się powyższe wzory oraz jak działa MATLABowska funkcja fit, która dopasowuje model do danych pomiarowych.

Metoda najmniejszej sumy kwadratów (LS - Least Squares)

Początki metody najmniejszej sumy kwadratów sięgają początku XIX wieku, kiedy A.M Legendre (1806) i K.F. Gauss (1809) niezależnie sformułowali jej podstawy. Metoda ta służyła do wyznaczania orbit planet i komet na podstawie obserwacji astronomicznych, jednak dzięki swej uniwersalności szybko zdobyła popularność w innych dziedzinach nauki niż mechanika nieba.

Polega ona na obliczeniu takich współczynników modelu (np. naszej prostej), które zapewniają minimalizację kryterium Q, będące liczbową miarą „odległości” pomiędzy danymi pomiarowymi, a dopasowywanym modelem:

Podstawiając za ym, przyjęty model liniowy otrzymujemy:

Kryterium Q, jest więc funkcją parametrów prostej b1 i b0. Aby to kryterium przyjęło wartość minimalną, czyli żeby nasz model, jak najmniej „odstawał” od danych pomiarowych, należy policzyć dwie pochodne, po b1 i bo, przyrównać je do zera i z tak stworzonego układu równań obliczyć wartości poszukiwanych współczynników:

skąd:

Mówimy, że b1 i b0 to estymatory LS współczynników, gdyż są to jedynie przybliżenia – ale o tym poniżej.

Poniżej znajduje się listing programu realizujący  dopasowanie modelu liniowego do danych pomiarowych. Same dane można pobrać tutaj.

clear all; close all; clc

load cz_pot2

N=length(u);

% wykres danych pomiarowych:
figure;
subplot(211); plot(u,y,'x','LineWidth',2);

%% OBLICZENIE WSPÓŁCZYNNIKÓW MODELU LINIOWEGO (estymator LS)

b1=(N*sum(u.*y)-sum(u)*sum(y))/(N*sum(u.^2)-sum(u).^2)
b0=(sum(y)-b1*sum(u))/N

% przyjęty model:
ym=b1*u+b0;

% model charakterystyki:
hold on; plot(u, ym,'r','LineWidth',2); 
xlabel('u'); ylabel('y'); grid on;
legend('dane pomiarowe', 'dopasowany model liniowy', 'location','northwest')

subplot(212);
bar(u, y-ym);
xlabel('u'); ylabel('y-ym'); grid on;

%% INNE OBLICZENIA
% suma różnic odpowiedzi obiektu i modelu
e=sum(y-ym)

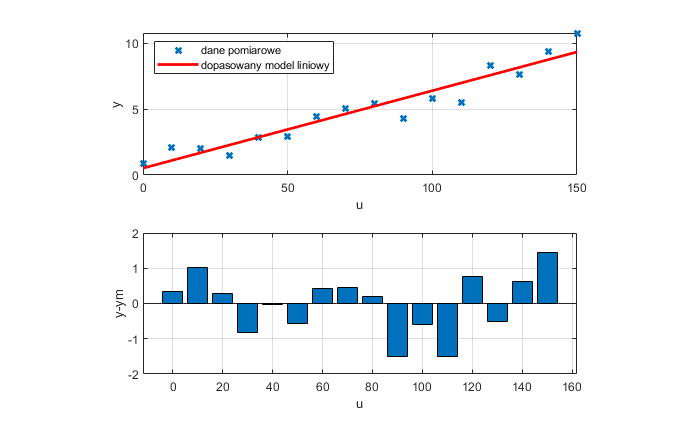
Cechą charakterystyczną metody LS jest to, że kryterium Q, czyli suma kwadratów różnic y i ym jest minimalna, natomiast suma różnic (bez podnoszenia do kwadratu) jest równa zeru.

Zobrazujmy na rysunku różnicę pomiędzy y i ym dla każdego argumentu u. Te różnice reprezentują „odległość” modelu od pomiaru dla każdego u. Są to tak zwane residua:

Residua mają różne znaki i ich suma, obliczona w MATLABie, zgodnie z teorią ma wartość bliską zeru. Sprawdźcie to w MATLABie.

MATLAB i funkcja fit

Funkcje toolboxa curve fiting, wykorzystują metodę LS do estymacji współczynników modeli aproksymujących dane pomiarowe. Oprócz modeli liniowych (jak w przykładzie powyżej) funkcja fit umożliwia użycie modeli wyższych rzędów, na przykład paraboli, itd. W takiej sytuacji współczynniki nie są dane wzorem, jak powyżej, lecz obliczanie algorytmem LS w postaci macierzowej. Wynika to z faktu, że analityczne (w postaci wzoru) wyznaczenie współczynników modeli wyższych rzędów jest trudne oraz nie jest uniwersalne – nie da się w programie „wpisać” wzorów na stałe dla modelu dowolnego rzędu. Jest więc potrzebny algorytm, który będzie uniwersalny.

Do tego celu służy macierzowy algorytm LS. Jego nazwa nawiązuje do tego, że w zależności od rzędu modelu, są tworzone macierze zawierające odpowiednio przekształcone wektory u i y. O tym jak to jest robione będzie traktował kolejny wpis na blogu.