Dyskretne przekształcenie Fouriera to król cyfrowego przetwarzania sygnałów. Wszyscy z niego korzystamy chociażby podczas wywoływania funkcji FFT w pakiecie MATLAB. Jakie są cechy tego przekształcenia oraz jak interpretować wyniki? Jak próbkowanie sygnałów wpływa na ich widmo częstotliwościowe? Na te i inne pytania związane z częstotliwościową analizą sygnałów znajdziecie odpowiedz w tym wpisie.
Na początku dwie uwagi: temat jest bardzo obszerny i trudno go przedstawić bez używania wzorów – stąd w tekście występują pewne uproszczenia i dzięki temu tylko jeden wzór 😊. Po drugie poprawnym określeniem jest transformacja Fouriera, jednak w Polsce potocznie zakorzeniło się używanie transformata Fouriera (efekt transformacji) i tej konwencji w nazewnictwie będę się trzymał 😊 Do rzeczy!
Jednym z najpopularniejszych postów na naszym blogu jest ten dotyczący transformaty Fouriera – potężnego narzędzia analizy sygnałów, które jest dostępne w pakiecie MATLAB. Z postu mogliście się dowiedzieć, że transformata Fouriera pozwala poznać strukturę częstotliwościową sygnałów. Innymi słowy, na przykład sygnał mowy zarejestrowany przez mikrofon podłączony do komputera, będący funkcją czasu (zapis słowa metrologia), taki jak ten:
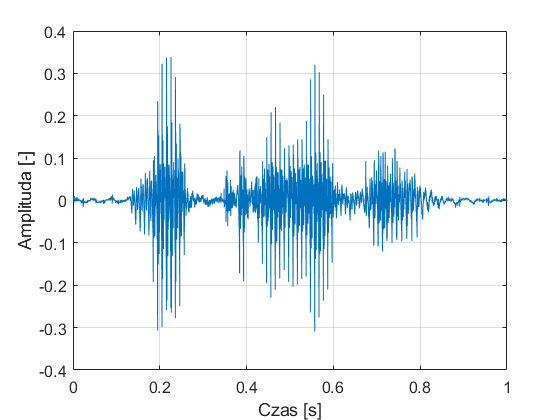
pozwala przedstawić w dziedzinie częstotliwości w taki sposób:
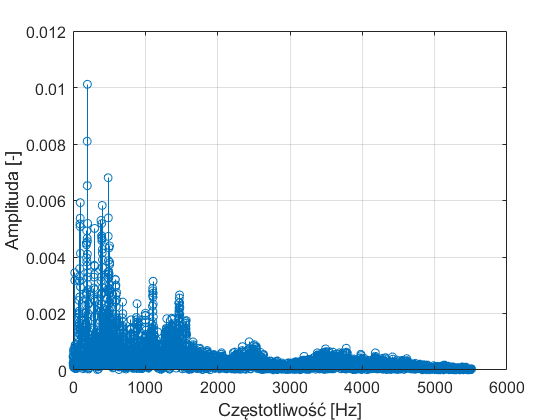
Powyższy obraz jest efektem narysowania modułu transformata Fouriera obliczonej za pomocą funkcji FFT. Widzimy, że sygnał zawierający zapis wymowy słowa metrologia zawiera częstotliwości głównie w zakresie do 2000Hz. Powiększając ten przedział częstotliwości możemy dostrzec, że w sygnale występują harmoniczne skupione wokół 100Hz, 200Hz, 300Hz, itd:
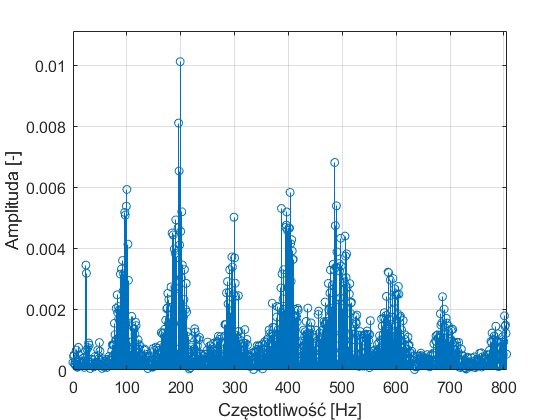
Jest to zgodne z intuicją, gdyż w słowie metrologia występują głównie głoski dźwięczne, „dzwoniące” przy określonych częstotliwościach. Jednak czy możemy być pewni poprawności wyniku uzyskanego na powyższym rysunku? Przecież wszystko zrobiliśmy poprawnie (użycie FFT), a wynik jest logiczny (interpretacja głosek dźwięcznych)…
Otóż okazuje się, że NIE.. Nie wolno nam „w ciemno” interpretować analizy widmowej, jeżeli nie znamy częstotliwości próbkowania sygnału! Może bowiem okazać się, że uzyskane wyniki nie są poprawne, a my popełniamy poważny błąd w interpretacji.
Transformata Fouriera
Dlaczego tak jest? Rozważmy następujący przykład: mamy dwa sygnały sinusoidalne o amplitudzie 1 i częstotliwościach 1Hz i 11Hz. Sygnały próbkujemy równomiernie z częstotliwością 20Hz – czyli na każdą sekundę trwania sygnału pobieramy 20 próbek. Zobaczmy jak wyglądają oryginalne sygnały ciągłe, oraz ich spróbkowane wersje – sygnały dyskretne. Poniżej znajduje się program i rysunki.
clear all; close all; clc
%% Generacja sygnałów "ciągłych"
% Musimy je "symulować" w MATLABie, gdyż w komputerze każdy sygnał jest
% dyskretny. Stąd słowo "ciągły" jest w cudzysłowie - efekt ciągłości
% uzyskujemy przez ustawienie dużej częstotliwości próbkowania.
% Robimy to tylko po to, aby móc narysować sygnały "ciągłe" na tle ich
% spróbkowanych odpowiedników. Sygnały "ciągłe" nie biorą udziału w analizie
% częstotliwościowej.
fpr_cont=10e3; dt_cont=1/fpr_cont; % wysoka częstotliwość próbkowania
to_cont=1; N_cont=to_cont/dt_cont; % czas obserwacji sygnałów
t_cont=(0:N_cont-1)*dt_cont; % wektor czasu "ciągłego"
f1_cont=1; fi1_cont=0; % częstotliwości i fazy sygnałów "ciągłych"
f2_cont=11; fi2_cont=0;
x1_cont = sin(2*pi*f1_cont*t_cont+fi1_cont); % generacja sygnałów "ciągłych"
x2_cont = sin(2*pi*f2_cont*t_cont+fi2_cont);
%% Generacja sygnałów dyskretnych (próbkowanie)
fpr=10; dt=1/fpr; % Częstotliwość i okres próbkowania
t0=1; N=t0/dt; % Czas obserwacji sygnałów i liczba próbek
t=(0:N-1)*dt; % Wektor czasu
df=fpr/N; F=df*(0:N-1); % Wektor częstotliwości do FFT
% Parametry sygnałów dyskretnych oczywiście takie jak ciągłych
f1=f1_cont; fi1=fi1_cont;
f2=f2_cont; fi2 = fi2_cont;
% Generacja sygnałów dyskretnych
x1 = sin(2*pi*f1*t+fi1);
x2 = sin(2*pi*f2*t+fi2);
%% Rysunki
figure;
plot(t_cont, x1_cont, t_cont, x2_cont)
hold on; plot(t, x1, 'ob', t, x2, 'or'); grid on;
title(['Sygnały: ' num2str(f1) ' oraz ' num2str(f2) ' [Hz]']);
xlabel('Czas [s]'); ylabel('Amplituda [-]')
set(findobj(gcf,'type','axes'),'FontName','Halvetica','FontSize',12);
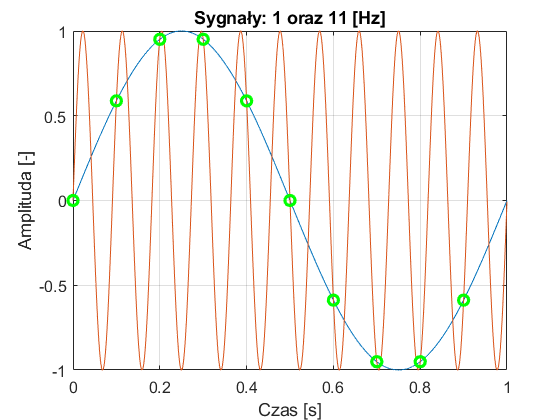
Z rysunku wynika, że ciąg próbek (zielone kółka) reprezentuje dwa sygnały! Próbki te mogą należeć do sygnału o częstotliwości zarówno 1Hz jak również 11Hz. Jest to bardzo ważna obserwacja. Okazuje się, że nie możemy bez niejednoznaczności określić częstotliwości sygnału na podstawie wartości próbek! Jak to możliwe i jakie ma to konsekwencje dla wyniku analizy widmowej? Dodajmy do powyższego programu fragment związany z obliczaniem FFT i narysujmy widmo obydwu sygnałów (moduł transformata Fouriera):
%% Obliczanie DFT z wykorzystaniem algorytmu FFT i rysunki
X1=(2/N)*abs(fft(x1));
X2=(2/N)*abs(fft(x2));
figure;
stem(F(1:N/2), X1(1:N/2));
hold on; stem(F(1:N/2), X2(1:N/2), 'r'); grid on;
legend(['Widmo sygnału o f1=' num2str(f1) 'Hz'],['Widmo sygnału o f2=' num2str(f2) 'Hz'])
xlabel('Częstotliwość [Hz]'); ylabel('Amplituda [-]');
set(findobj(gcf,'type','axes'),'FontName','Halvetica','FontSize',12);
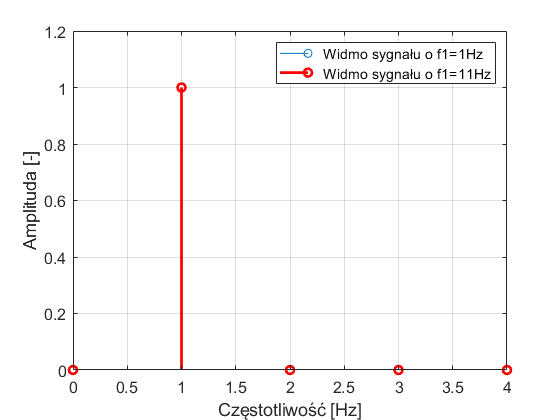
Widma obydwu sygnałów o różnych częstotliwościach (1Hz i 11Hz) są identyczne i nałożyły się na siebie. Sygnał o częstotliwości 11Hz jest błędnie reprezentowany przez prążek o częstotliwości 1Hz. Dlaczego tak się stało? Pełne wytłumaczenie tego zjawiska wymaga przeprowadzenia dowodu matematycznego. Znajdziecie go w każdej książce do przetwarzania sygnałów. Polecam przestudiować ten dowód, bo jest piękny w swej prostocie. Nie wchodząc jednak w zawiłości matematyczne, dla praktyków ważne jest poniższe stwierdzenie:
Nie jesteśmy w stanie rozróżnić spróbkowanych wartości sygnału sinusoidalnego o częstotliwości f0 oraz sygnału sinusoidalnego o częstotliwości f0+k*fpr, gdzie k jest dowolną liczbą całkowitą.
Jeżeli k może być dowolną liczbą całkowitą, oznacza to, że ciąg próbek może reprezentować nieskończoną liczbę sinusoid o częstotliwościach określonych powyższym wzorem! Jest to fundamentalne twierdzenie analizy częstotliwościowej, o którym należy pamiętać za każdym razem, kiedy używamy w pakiecie MATLAB funkcji FFT i innych, które ten algorytm wykorzystują.
Skąd zatem możemy mieć pewność, że wykonana przez nas analiza jest poprawna (jak dla sygnału o częstotliwości 1Hz) bądź błędna (jak dla sygnału o częstotliwości 11Hz, który został błędnie zinterpretowany jak 1Hz)? Te pytania prowadzą nas w kierunku twierdzenia o próbkowaniu, które mówi o tym jaka powinna być częstotliwość próbkowania sygnału dolnopasmowego, aby jego widmo zostało wyznaczone w poprawny sposób, tj. bez niejednoznaczności w dziedzinie częstotliwości.
O tym możecie przeczytać TUTAJ 😊
Dodatek
PS. Na koniec kilka definicji dla dociekliwych. Ich poznanie pozwoli Wam uporządkować nieco wiedzę:
Szereg Fouriera – szereg umożliwiający przedstawienie sygnału ciągłego w czasie, jako sumy składowej stałej oraz składowych harmonicznych o różnych częstotliwościach. Jest to metoda analizy częstotliwościowej sygnałów ponieważ współczynniki szeregu Fouriera informują nas jakie częstotliwości występują w sygnale, a jakie nie.
Próbkowanie równomierne sygnału analogowego (ciągłego) – operacja polegająca na wyborze wartości z sygnału ciągłego w ściśle określonych chwilach czasu odległych od siebie o czas zwany okresem próbkowania dt. Odwrotność dt, to częstotliwość próbkowania fpr wyrażona w hercach [Hz]. Proces próbkowania sygnału jest niezbędny aby poddać go analizie cyfrowej. Sygnał spróbkowany nazywamy sygnałem dyskretnym.
DFT – Discrete Fourier Transform – dyskretna transformacja Fouriera lub inaczej dyskretne przekształcenie Fouriera (potocznie nazywane transformata Fouriera) – jest to odpowiednik szeregu Fouriera dla sygnałów dyskretnych. Z takimi sygnałami mamy do czynienia w pakiecie MATLAB, niezależnie czy analizujemy zapisany za pomocą karty pomiarowej sygnał, czy sami go generujemy za pomocą funkcji takich jak np. sin.
FFT – Fast Fourier Transform – algorytm obliczający w efektywny sposób DFT.