Autorem tego wpisu jest Błażej Roch Żyliński. Najemny innowator i wynalazca. Seryjny przedsiębiorca. Brał udział w ponad 100 projektach badawczo-rozwojowych. Absolwent Lotnictwa i Kosmonautyki na Wydziale MEiL oraz Automatyki, Robotyki i Informatyki Przemysłowej na Wydziale Mechatroniki PW. Pracował w Centrum Badań Kosmicznych PAN i współpracował z partnerami takimi jak Airbus czy AGH w Krakowie.
Kolor liczby to pewna umowa. Tak jak kolory kwarków z tą różnicą, że w mechanice kwantowej niczym dziwnym jest powiedzieć, że kwark ma kolor zielony albo anty-niebieski. Kto nam jednak zabroni trochę na ten temat dywagować?
W matematyce nie mówi się o kolorach liczb, ale danym kolorom te liczby się przypisuje.
Przykładem takiego przyporządkowania jest model RGB, skrót od angielskich słów
R - red (czerwony)
G - green (zielony)
B - blue (niebieski)
Jeżeli chcesz zdefiniować kolor wykresu w MATLABie to używasz właśnie skali RGB, choć w nieco zmienionej formie. Wartości poszczególnych kolorów są wyrażone w skali od 0 do 1 lub jako liczba w systemie szesnastkowym (hex).
Jak w takim razie możemy wskazać kolor liczby Pi?
Potrzebujemy wektora o trzech składowych przyjmujących wartości od 0 do 1.
Liczba Pi jakiej używamy na co dzień zapisana jest w systemie dziesiętnym.
Skoro musimy przyporządkować wartości do wektora o wymiarze trzy warto przejść z systemu o podstawie 10, na system o podstawie 3. System o podstawie 3 składa się z trzech cyfr 0, 1 i 2.
W takim razie załóżmy, że R to zera, G to jedynki, a B to dwójki.
MATLAB potrafi zamieniać liczby z jednego systemu liczbowego na drugi. Wykorzystywana do tego jest funkcja dec2base(), ale obsługuje ona tylko liczby całkowite. Wykonanie takiej operacji dla liczb ułamkowych (z częścią po przecinku) wymaga napisania własnej funkcji. Liczba Pi nie dość, że jest niewymierna to do tego nie jest okresowa.
Mamy w takim razie dwie opcje: znaleźć rozwinięcie liczby Pi w systemie trójkowym albo napisać własny fragment kodu, który takiej sztuki dokona.
Tym razem wygrał mój pragmatyzm - to chyba dobrze, bo MATLAB jest przeznaczony dla inżynierów, a z natury są to osoby pragmatyczne i wykorzystujące dostępne narzędzia. Znalazłem stronę, która pozwoliła mi na wyrażenie rozwinięcia liczby Pi = 3.141592 w systemie trójkowym.
Niemniej pozostaje to ciekawe zadanie programistyczne - warte poruszenia w osobnym wpisie.
W systemie trójkowym liczba Pi wygląda następująco: 10.0102110122. Możliwe, że zalała Cię teraz fala oburzenia. Dlaczego proponuję tak krótkie rozwinięcie dla liczby o nieskończonym rozwinięciu? Już spieszę z odpowiedzią.
Zgodzisz się ze mną, ze liczbie Pi jest bliżej do 3 niż do 4. Tak samo w zapisie trójkowym jest to bardziej 10 niż 11. W takim razie zasadne jest przypisywanie poszczególnym pozycjom wag.
To tym bardziej istotne, że zbiory zer, jedynek i dwójek nieskończonego rozwinięcia liczby Pi będą prawdopodobnie niemal równoliczne. Tak na inżynierski rozum. Może jakiś informatyk albo matematyk tę hipotezę obali. Niemniej tak jest w przypadku rozwinięcia dziesiętnego:
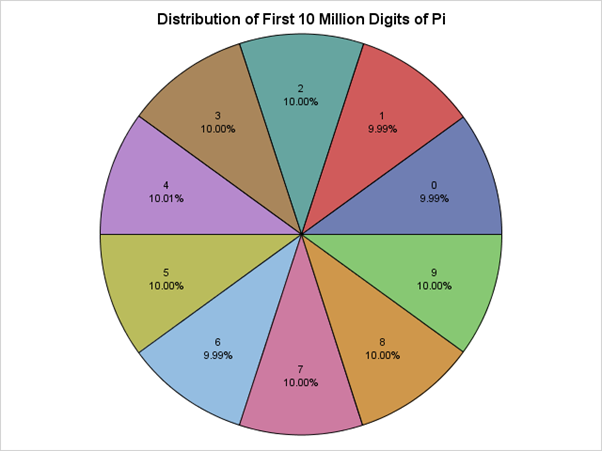
Rozkład pierwszych 10 milionów cyfr liczby Pi zapisanej w systemie dziesiętnym. Źródło: https://blogs.sas.com/content/iml/2015/03/12/digits-of-pi.html
Gdyby wagi dla wszystkich cyfr były równe to uzyskalibyśmy RGB [1 1 1] czyli biały.
Z uwagi, że mamy do czynienia z systemem o podstawie 3 wagi dla poszczególnych pozycji wyglądają następująco: (⅓)^0, (⅓)^1, (⅓)^2, … , (⅓)^(i-1) gdzie i jest pozycją cyfry w zapisie trójkowym licząc od lewej strony.
Teraz jest już oczywiste, że analizowanie rozwinięcia Pi z dziesiątkami czy setkami cyfr nie ma sensu. Ostatnia waga w naszym przykładzie, czyli (⅓)^11 daje 5,6450292694767622370121989082513e-6
Wszystko wyjaśnione, pozostało przejść do liczenia.
Najpierw musimy zmienić naszą “trójkową” liczbę Pi na wektor, który pozwoli nam na iterowanie kolejnych pozycji.
pi_vec = [1 0 0 1 0 2 1 1 0 1 2 2]
pi_vec =
1 0 0 1 0 2 1 1 0 1 2 2
Potrzebujemy również macierzy c, w której będziemy zliczać wagi naszego koloru.
c=zeros(1,3)
c =
0 0 0
Pętla wygląda następująco:
for i=1:length(pi_vec)
if pi_vec(i) == 0
c(1)=c(1)+(1/3)^(i-1);
elseif pi_vec(i) == 1
c(2)=c(2)+(1/3)^(i-1);
else pi_vec(i) == 2
c(3)=c(3)+(1/3)^(i-1);
end
end
To jednak nie wszystko. Jak widzisz wektor c zawiera wartość większą niż jeden.
c =
0.45694 1.0389 0.0041378
Musimy w takim wypadku go znormalizować. Wykorzystując funkcję max() znajdujemy największa składową wektora c.
m=max(c) %funkcja znajdująca największą wartość w wektorze
m =
1.0389
Pozostaje nam już tylko podzielić przez nią wszystkie składowe.
c_n=c/m %normalizacja wektora
c_n =
0.43983 1 0.0039828
To już ten moment. Zaraz poznamy kolor liczby Pi.
% Wykres prezentujący kolor liczby Pi
x = [0 1 1 0] ; y = [0 0 1 1] ;
figure('Name','Kolor liczby Pi')
fill(x,y,c_n)
Co w efekcie daje nam wykres w formie kwadratowego pola o pożądanym kolorze (rys. 2).
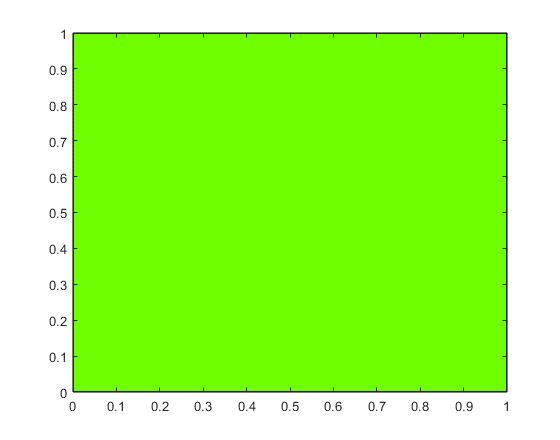
Wyszedł nam kolor jasnozielony. Czy ten kolor ma unikatową nazwę?
W Wikipedii znajdziesz listę nazw kolorów w języku polskim. Poza nazwami lista
zawiera opis kolorów w RGB i systemie szesnastkowym (Hex): https://pl.wikipedia.org/wiki/Lista_kolorów
W takim razie musimy pomnożyć nasz znormalizowany wektor przez 255:
format shortG c_n_bit = [0.439825908357377 1.000000000000000 0.003982808178612]*255
c_n_bit =
112.16 255 1.0156
RGB wykorzystuje liczby całkowite, w związku z tym zaokrąglamy wartości naszego wektora do liczb całkowitych wykorzystując funkcję round():
c_round = round(c_n_bit) c_round = 112 255 1
Nie jest to jednak wygodna forma do szukania na takiej liście. Ctrl + F nie zadziała.
Zapis w systemie szesnastkowym będzie wygodniejszy. W tym celu wykorzystujemy funkcję dec2hex. Tym razem możemy jej użyć, bo operujemy na liczbach całkowitych.
dec2hex(c_round)
ans =
3×2 char array
'70'
'FF'
'01'
Mamy to!
Niestety radość jest przedwczesna…
Okazuje się, że kolor #70FF01 nie ma nazwy i nie znajduje się na liście.
Czy w takim wypadku przysługuje mi prawo do nazwania tego koloru? Jeżeli tak to proponuję by nazywał się pi zielony.
Może masz inną propozycję nazwy koloru lub wskażesz kolor, który najbardziej przypomina pi zielony? Daj znać w komentarzu!

