Czternasty marca to Światowy Dzień Liczby Pi, liczby chyba najważniejszej w matematyce. To pi pojawia się często w nieoczekiwanych okolicznościach. Dzięki temu jest świetną okazją do zwrócenia uwagi na inne działy matematyki. W tym roku zastanowimy się ile wynosi silnia z liczby pi.
Pojęcie silni możecie
kojarzyć przede wszystkim z kombinatoryki.
n! to tak zwana permutacja bez powtórzeń. Odpowiada na
pytanie - na ile sposobów możemy ułożyć zbiór różnych n elementów złożony ze
wszystkich elementów tego zbioru?
Zbiór A = [a,b,c} da się ułożyć na poniższe sposoby:
abc
acb
bac
bca
cab
cba
czyli 3! = 123 = 6
Zbiór liter polskiego alfabetu - nie licząc q, v i x - możemy ułożyć na 32! konfiguracji. Liczenie ręcznie byłoby bardzo żmudne, ale dzięki MATLABowi wystarczy, że wpiszemy polecenie:
factorial (32)
i otrzymujemy wynik
ans =
2.631308369336935e+35
To bardzo duża liczba. Jej rząd to aż 10 do 35-tej potęgi. Wypisanie wszystkich możliwości ręcznie jak w poprzednim przykładzie byłoby niemożliwe. Operacja silni daje bardzo duże liczby. Okazuje się jednak, że MATLAB potrafi policzyć nawet silnię ze 170.
factorial(170)
ans =
7.257415615307994e+306
Czy ta liczba jest duża? Liczba atomów w obserwowalnym Wszechświecie jest szacowana na od 10^78 do 10^82. W związku z tym 170! jest wartością więcej niż kosmiczną. Dla znakomitej większości przypadków z zupełności wystarczającą.
Spróbujmy obliczyć silnię ze 171:
factorial(171)
MATLAB zwróci wartość:
ans =
Inf
Jest to spowodowane tym, że 171! daje liczbę przekraczającą maksymalną wartość możliwą do przedstawienia jako double.
Silnia z pi, czyli silnia liczby rzeczywistej
Zgłębiliśmy możliwości MATLABa jeżeli chodzi o liczenie silni, przejdźmy zatem do obliczania silni z liczby pi.
Wpisujemy f=factorial(pi) i niestety otrzymujemy poniższy komunikat:
Error using factorial
N must be an array of real non-negative integers.
Funkcja factorial() pozwala na policzenie silni tylko z nieujemnej liczby całkowitej
Czy można zatem obliczyć silnię z liczby rzeczywistej?
Okazuje się, że tak. Trzeba jednak użyć do tego specjalnej metody. Konkretnie wykorzystać funkcję specjalną gamma zwaną też funkcją gamma Eulera. Jedną z metod jej wyznaczenia jest policzenie tzw. całki Eulera II rodzaju, która wygląda następująco:
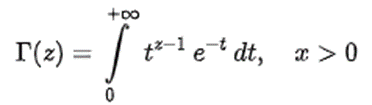
gdzie z = x + iy, czyli jest liczbą zespoloną.
Policzenie takiej całki wymaga już sporo wiedzy i wysiłku, ale na całe szczęście nie musimy się tym kłopotać. MATLAB ma wbudowaną funkcję gamma. Wystarczy zapisać:
gamma(1+pi)
i otrzymujemy
ans =
7.188082728976031
Od razu spieszę z wyjaśnieniem, że pomiędzy funkcją gamma, a silnią istnieje następujący związek:
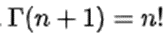
Dlatego do liczby pi musieliśmy dodać jeden.
Okazuje się, że funkcja gamma ma jeszcze jedną niezwykłą właściwość, która wiąże ją bezpośrednio z liczbą pi.
Otóż Γ(0.5) równe jest √π. Możemy to łatwo sprawdzić w MATLABie wyliczając odpowiednią różnicę:
c=gamma(0.5)-sqrt(pi)
c =
2.220446049250313e-16
Wartość różnicy jest bardzo mała i wynika z przybliżenia, jakie stosuje środowisko MATLAB. Dla inżynierów raczej nie ma to znaczenia, matematycy udowodnili, że różnica wynosi zero.
W nauce i technice bardzo dobrą metodą komunikacji są wykresy. Z MATLABem ich przygotowanie jest niezwykle proste. Wykreślimy teraz funkcję gamma i naniesiemy kilka początkowych wartości silni w zakresie od 1 do 5. Przygotowujemy odpowiedni kod:
x=1:0.1:5.1;
g=gamma(x+1);
n=1:1:5;
s=factorial(n);
plot(x,g,n,s,'o','MarkerSize',6,'MarkerFaceColor','r')
grid on
grid minor
title('Silnia i funkcja Gamma')
legend ('funckja Gamma','silnia','Location','North')
i otrzymujemy wykres:
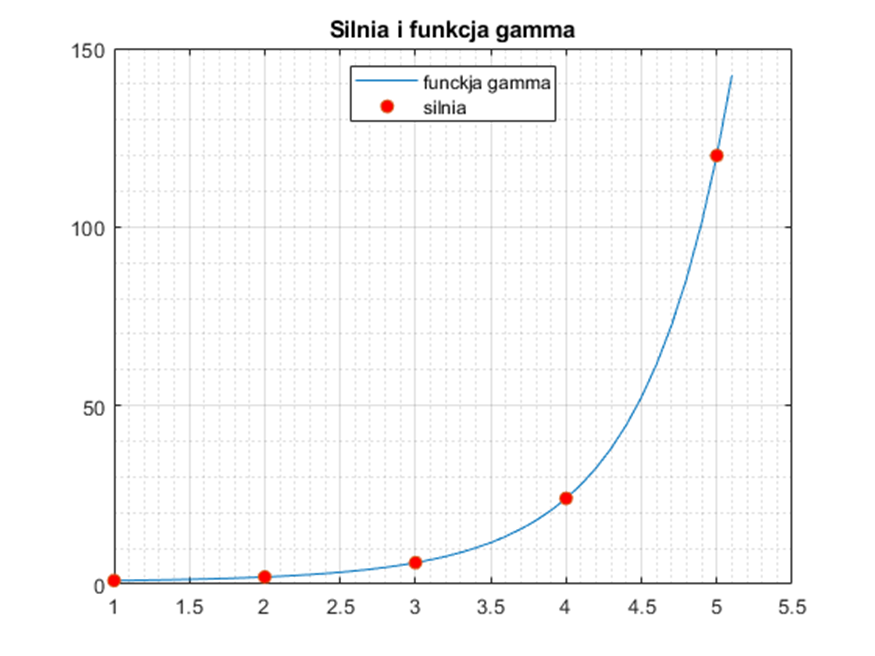
Jak widzicie, wartości silni dla liczb całkowitych pokrywają się z funkcją gamma.
Warto mieć świadomość, że dziedzina funkcji gamma obejmuje również liczby ujemne, ale jest ona nieokreślona w punktach 0, -1, -2…
Funkcja gamma dla argumentów od -5 do 5 prezentuje się tak:

Wykres uzyskaliśmy z pomocą poniższego kodu:
x=-5:0.001:5;
g=gamma(x);
plot(x,g)
ylim([-10 10])
ax = gca;
ax.XAxisLocation = 'origin';
ax.YAxisLocation = 'origin';
grid on
grid minor
title('Funkcja gamma dla argumentów <-5, 5>')
Możemy za to sprawdzić, ile wynosi silnia z minus pi. Wpisujemy formułę:
gamma(1-pi )
i otrzymujemy
-3.190906687308356
Zastosowania funkcji gamma Eulera
Nasuwa się pytanie, do czego możemy wykorzystać funkcję gamma. Okazuje się, że ma ona szereg zastosowań. Pozwala nam m.in. policzyć pochodną ułamkowego rzędu np. 3/2.
O zastosowaniach rachunku różniczkowego ułamkowego rzędu w automatyce możesz usłyszeć w podcaście Szlak B + R z udziałem dr. inż. Jakuba Możaryna z Wydziału Mechatroniki Politechniki Warszawskiej: https://youtu.be/gtE08trcL-w?si=2TxoxVorpDtJaqrR
Funkcję gamma Eulera stosuje się również w mechanice płynów i fizyce kwantowej. Na jej podstawie definiuje się rozkład gamma - narzędzie statystyczne przydatne m.in. w onkologii i neurologii.
Służy również do sformułowania innej słynnej funkcji, funkcji dzeta Riemanna:

Funkcja dzeta posłużyła Bernhardowi Riemannowi do sformułowania słynnej hipotezy dotyczącej liczb pierwszych. Znajdziecie ją również w MATLABie jako zeta().
Cudowną cechą matematyki są wzajemne powiązania jej różnych działów. Powyżej podałem jedynie jeden z wielu przykładów. Możemy powiedzieć, że i tym razem bardzo abstrakcyjne rozważania matematyczne znalazły praktyczne zastosowanie w nauce i technice.
Dzień liczby pi to święto królowej nauk - matematyki. Dzięki MATLABowi możesz stosować wielowiekowy dorobek królowej nauk bez zbędnego wysiłku jednocześnie czerpiąc z tego korzyści.
Autorem wpisu jest Błażej Żyliński. Łączy świat nauki i biznesu. Specjalizuje się w obszarach sztucznej inteligencji , Internetu Rzeczy, zarządzania energią, inteligentnych miast, robotyki i kosmonautyki. Entuzjasta technologii kwantowych.

