Choć MATLAB może być traktowany jako język programowania, na pewno może zaskoczyć nietypowymi, dla "rasowego" programisty rozwiązaniami. Idea jest w zasadzie taka, by użytkownik środowiska MATLAB analizując dane nie musiał uciekać się na każdym kroku do tworzenia funkcji pomocniczych i wykorzystywania konstrukcji programistycznych takich jak pętle i instrukcje warunkowe. One w MATLABie oczywiście istnieją i są w wielu sytuacjach niezbędne, jednak wiele można zrobić bez nich.
Poszukiwanie maksimum
W poprzedniej części samouczka udało Ci się zidentyfikować lipiec 2003 roku jako nietypowy, pod względem liczby oddanych do użytku w Polsce mieszkań, miesiąc. Problem polega na tym, że w celu identyfikacji tego określonego w czasie punktu trzeba było dokładnie przeanalizować wykres. Oczywiście, analiza wykresów to w zasadzie podstawa pracy z każdymi danymi, jednak optymalnie byłoby po zerknięciu na wykres wydobyć informacje o interesujących nas punktach w sposób przynajmniej częściowo zautomatyzowany. Zacznijmy jednak (prawie) od początku.
- Wczytaj dane zebrane w pliku bud.mat,
- Z macierzy BMdaneM wybierz dane dotyczące miesięcznej łącznej liczby oddanych do użytku mieszkań (ogółem) i zapisz je jako wektor w zmiennej ogolemV
- Wygeneruj wektor czasu odpowiadający długością wektorowi ogolemV
- Umieść dane na wykresie.
load bud ogolemM = BMdaneM(2:6:end,:)'; % wybranie danych i transpozycja (operator - apostrof) ogolemV = reshape(ogolemM, [], 1); ogolemV = ogolemM(:); % alternatywna metoda t1 = datetime(1991,1,31) dt = calendarDuration(0,1,0) N = length(ogolemV); % zapisanie informacji o długości wektora t = t1:dt:t1+(N-1)*dt; plot(t, ogolemV);
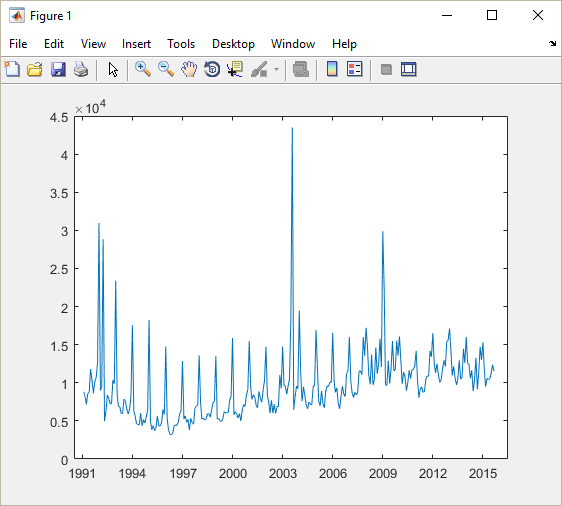
W kodzie przedstawionym powyżej zaszło kilka zmian względem tego, co można znaleźć w Matlab Tutorial #5. Przestawiam zatem kilka wyjaśnień.
ogolemV = ogolemM(:); % alternatywna metoda
Zgodnie z tekstem dodanym jako komentarz po znaku '%', jest to alternatywny sposób przekształcenia macierzy ogolemM w wektor. W przypadku funkcji reshape użytkownik może określić, jakie maja być wymiary macierzy wynikowej, w przypadku wykorzystania operatora (:) wynikiem zawsze jest wektor o rozmiarach Nx1. Inaczej rzecz ujmując, cała zawartość macierzy trafia do jednej kolumny.
N = length(ogolemV); t = t1:dt:t1+(N-1)*dt;
Dzięki zastosowaniu funkcji length w zmiennej N została zapisana długość wektora ogolemV. Pisząc ten poradnik opieram się na danych z końca roku 2015, zawartych w pliku mieszkania_91_15.xls Prawdopodobnie w kolejnych latach pliki umieszczane na stronach Głównego Urzędu Statystycznego będą uzupełnianie o nowe dane i wielkości macierzy BMdaneM tworzonej na podstawie wskazówek umieszczonych w Matlab Tutorial #3 może wzrosnąć. Wprowadzenie do procesu przetwarzania zmiennej N ma na celu uniezależnienie tworzonego kodu od wielkości macierzy. Dzięki temu, jeśli zaczniesz przerabiać ten turorial na początku roku 2017, a GUS udostępni w międzyczasie dodatkowe dane, również one mogą być uwzględnione w analizie. Wektor t nie jest tworzony na sztywno. Ostatnia data, jak się w nim znajdzie, jest wyliczana na podstawie ilości elementów wektora ogolemV.
Odszukanie wartości maksymalnej to oczywiście żaden problem, wystarczy wykorzystać przedstawioną już wcześniej funkcję max.
m = max(ogolemV);
To niestety jednak tylko część sukcesu. Wiemy już jaka była maksymalna wartość, ale nie wiemy ciekawszej rzeczy, kiedy ta wartość została osiągnięta.
Wielokrotne argumenty wyjściowe funkcji
Okazuje się, że w MATLABie funkcja max może zwrócić nam dwie informacje.
- Jaka jest wartość maksymalna.
- Gdzie ta wartość maksymalna się znajduje (w którym miejscu macierzy).
I właśnie to jest nam potrzebne. Jeśli funkcja ma zwrócić więcej niż jeden argument wyjściowy, wszystkie nazwy zmiennych, które mają służyć do przechowywania wyniku, należy umieścić w nawiasach kwadratowych po lewej stronie znaku równości.
- zastosuj funkcję
maxna wektorze ogolemV zapisując wynik do dwóch argumentów wyjściowych - wykorzystaj drugi argument wyjściowy do wyznaczenia daty ("zaindeksowania" wektora t)
[m, idx] = max(ogolemV); x = t(idx)
x =
31-Jul-2003
Dobrze zapamiętać, że w MATLABie pojedyncza funkcja może bardzo często zostać wykorzystana na wiele różnych sposobów. Należy tylko odpowiednio operować argumentami wejściowymi i wyjściowymi.
Poza olbrzymim pikiem z lipca 2003 na wykresie widać jeszcze kilka ciekawych punktów, których wartość przekracza 20000. Jak je poprawnie zidentyfikować? W MATLABie jest to niezwykle łatwe dzięki technice indeksowania logicznego. Zanim do tego przejdziemy, należy jednak powiedzieć (w moim przypadku raczej napisać) parę słów o operacjach logicznych.
Operacje logiczne
Poza tym, że liczby w MATLABie możemy dodawać, dzielić, pierwiastkować itp. możemy je również porównywać. Przykładowo, może zainteresować nas, czy liczba liczba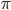 
jest większa od 3.
pi > 3
ans =
1
W wyniku pojawiła się jedynka, co oznacza prawdę. Konkretnie, nasze zdanie pi > 3 jest prawdziwe. Nic nie stoi na przeszkodzie, by wynik operacji logicznej zapisać do zmiennej.
x = pi <= 3
Po wykonaniu powyższego kodu do zmiennej x zostanie zapisane 0, co oznacza fałsz. Dzięki temu wiemy, że pi nie jest mniejsze lub równe 3. To ile może wynosić liczba pi?
x = pi == 3.14
Powyższy kod umożliwia sprawdzenie, czy liczba pi wynosi 3.14 (operator przyrównania to == ). Odpowiedzią jest fałsz, gdyż MATLAB przechowuje wartość liczby pi z nieco większą dokładnością. Bez jakiejś zbędnej przesady, ta dokładność to 15 miejsc po przecinku.
Możliwe jest tworzenie całych macierzy logicznych zer i jedynek. Można to robić "ręcznie":
x = [true false true]
Zazwyczaj jednak takie macierze powstają jako wynik operacji logicznych przeprowadzanych na macierzach liczbowych.
- Przy pomocy funkcji
randwygeneruj macierz losową r o rozmiarach 3 x 3 - Sprawdź, które elementy macierzyr mają wartość większą od 0.5
r = rand(3) x = r > 0.5
r =
0.8147 0.9134 0.2785
0.9058 0.6324 0.5469
0.1270 0.0975 0.9575
x =
1 1 0
1 1 1
0 0 1
Indeksowanie logiczne
W tym momencie dochodzimy do najciekawszej części. Macierze i wektory logiczne w MATLABie mogą posłużyć do indeksowania innych macierzy. Warunek jest taki, że rozmiar macierzy indeksującej i indeksowanej musi być taki sam. Jak to wykorzystać w praktyce? Dla przykładu, możemy teraz "wyzerować" wszystkie elementy macierzy r, które spełniają warunek >0.5. To częsty scenariusz w przypadku pracy z algorytmami, które wykorzystują progowanie.
r(x) = 0
r =
0 0 0.2785
0 0 0
0.1270 0.0975 0
Wpisując powyższy kod wydajemy polecenie: W macierzy r wstaw 0 na wszystkich pozycjach, na których w macierzy x znajduje się 1.
Wróćmy do naszych danych związanych z budownictwem mieszkaniowym. Jeśli wstępny przykład nie jest do końca czytelny, to teraz wszystko powinno się rozjaśnić. Przypominam jakie stoi przed nami zadanie, chcemy zidentyfikować wszystkie miesiące, w których liczba oddanych do użytku mieszkań przekraczała 20000. Pomińmy od razu lipiec 2003 roku, ten punkt mamy już przeanalizowany.
- Utwórz wektor logiczny idx, w którym jedynki wskażą miesiące dla których liczba oddanych do użytku mieszkań przekroczyła 20000 i jedocześnie jest mniejsza od 43492 (wartość maksymalna z lipca 2003 wyznaczona już dzięki funkcji
max) - Sprawdź, ile jest takich miesięcy.
idx = (ogolemV > 20000) & (ogolemV < 43492); % & - iloczyn logiczny sum(idx)
ans =
5
Operator & odpowiada za przeprowadzenie operacji iloczynu logicznego (Suma logiczna jest realizowana dzięki operatorowi | ). Teraz kluczowy moment, chcemy dowiedzieć się w jakich miesiącach spełniony został postawiony przez nas warunek oraz ile dokładnie mieszkań zostało wtedy oddanych do użytku. Do realizacji naszego celu możemy wykorzystać wektor logiczny idx.
t_powyzej20000 = t(idx) oddanych_powyzej2000 = ogolemV(idx)' %transpozycja kosmetyczna
t_powyzej20000 =
31-Dec-1991 31-Mar-1992 31-Dec-1992 31-Dec-2008 31-Jan-2009
oddanych_powyzej2000 =
30960 28833 23395 29877 22096
Indeksowanie logiczne to naprawdę niezwykle skuteczna i zarazem prosta technika wydobywania potrzebnych informacji z zestawu danych. Powyżej zrealizowaliśmy jeden ze standardowych scenariuszy; wyławiamy interesujące nas zdarzenie i identyfikujemy, kiedy miało ono miejsce. Możemy równie dobrze zadziałać w drugą stronę. Przypuśćmy, że z naszego wektora ogolemV potrzebne są nam informacje dotyczące wyłącznie trzech miesięcy: kwietnia, maja i czerwca. Można by było w tym momencie sięgnąć po macierz BMdaneM ale załóżmy, że do dyspozycji mamy jedynie wektory ogolemV i t i tylko na nich możemy operować.
Zanim przejdziemy do operacji logicznych, wymagane będzie drobne przekształcenie wektora t.
kwartal = quarter(t)
Dzięki metodzie quarter z wektora t wyciągnęliśmy tylko to, co nas interesuje, czyli numer kwartału (dostępne są również metody month, year i day). Teraz można przeprowadzić operację logiczną - szukamy wyłącznie kwartału oznaczonego liczbą 2.
idx = (kwartal == 2);
Ostatni krok to wykorzystanie wektora idx do zaindeksowania wektora ogolemV:
ogolem_q2= ogolemV(idx); histogram(ogolem_q2);