Automatyczna klasyfikacja obiektów bez nadzoru człowieka to jedno z zadań jakie stawia się przed algorytmami uczenia maszynowego. Z artykułu dowiecie się jak działają takie algorytmy oraz jak napisać program w MATLABie, który z wykorzystaniem samouczącego się algorytmu k-Means będzie dokonywał klasyfikacji obiektów.

Po dawce teorii z poprzedniego wpisu czas przejść do przykładów. Dzisiaj zajmę się jednym z podstawowych zagadnień uczenia maszynowego czyli automatycznej klasyfikacji obiektów, na podstawie oceny ich charakterystycznych cech. Przykładem takiego zadania może być klasyfikacja obiektów na duże, średnie, małe na podstawie pomiarów ich wymiarów, klasyfikacja pacjentów na chorych i zdrowych na podstawie wyników badań czy poruszony w tym artykule problem klasyfikacji pojazdów na podstawie rozstawu ich osi na osobowe i busy.

Klasyfikacja klasyczna

Klasyczny algorytm klasyfikacji działa podobnie do tego w jaki sposób człowiek ocenia przynależność elementu do danej klasy. Najpierw wybieramy zestaw cech na podstawie których będziemy przeprowadzać klasyfikacje (na przykład masa, długość, itp.) a następnie musimy określić zakres wartości każdej z cech, charakterystyczny dla rozpatrywanych klas. Człowiek zazwyczaj robi to intuicyjnie, „czując” gdzie są granice pomiędzy cechami elementów różnych klas. Komputer nie posiada jednak intuicji i potrzebuje danych wejściowych w postaci liczb. Liczby te definiują granice pomiędzy różnymi klasami i w klasycznym podejściu są ustalane przez człowieka na początku procesu. Algorytm jest więc zdeterminowany i nie posiada zdolności uczenia się. Na przykład, zakładając, że chcemy dokonać klasyfikacji z podziałem na dwie klasy, to definicja przedziałów wartości cech elementów może wyglądać następująco:

Klasa 1 charakteryzuje się:

Masa1=[od 1kg do 2kg], Długość1=[od 2m do 3m]

Klasa 2 charakteryzuje się:

Masa2=[od 2kg do 3kg], długość=[od 3m do 4m]

Teraz, wiedząc jakie cechy ma każda klasa, algorytm może dokonać klasyfikacji. Na przykład:

Element_1 ma cechy: masa=1.5kg, długość=3m --- klasyfikacja do Klasy 1

Element_2 ma cechy: masa=1kg, długość=2.5m --- klasyfikacja do Klasy 1

Element_3 ma cechy: masa=2.3kg, długość=3.5m --- klasyfikacja do Klasy 2

… i tak dalej.

Uczenie maszynowe

Z pomocą przychodzi algorytm uczenia maszynowego bez nadzoru k-Means. Nie wymaga on żadnych informacji wstępnych o cechach poszczególnych klas, gdyż w procesie uczenia się, rozpoznaje je sam. Jedyna informacja dostarczana przez człowieka, poza zbiorem danych do klasyfikacji, to liczba klas k na które chcemy podzielić nasz zbiór. Ponieważ w przypadku uczenia maszynowego używa się pojęcia klaster (cluster) zamiast klasa, to taka nomenklatura będzie występować w dalszej części artykułu.

Algorytm k-Mean

W przeciwieństwie do podejścia klasycznego, opisanego powyżej, w algorytmie k-Means nie ma z góry zdefiniowanych przedziałów wartości cech, charakterystycznych dla danej klasy/klastra. Magia uczenia maszynowego bez nadzoru polega na tym, że algorytm w procesie iteracyjnym, sam ocenia i koryguje (jeżeli jest potrzeba) granice wyznaczające cechy danego klastra. Innymi słowy algorytm k-Means sam rozpoznaje i klasyfikuje elementy o podobnych cechach, bez udziału człowieka.

Algorytm klasyfikuje badane elementy w klastry, za kryterium przyjmując „odległość” elementu od „środka” klastra. Tu należy użyć wyobraźni, gdyż nie chce wchodzić w szczegóły matematyczne. Ale odległość między dwoma elementami w najprostszym przypadku można rozumieć klasycznie, jako euklidesową miarę odległości. Natomiast „środek” klastra to wartość średnia cech elementów w klastrze. 

W skrócie, algorytm działa następująco:

1. weź dane wejściowe, które mają podlegać klasyfikacji i wyznacz k (losowo) wybranych „środków” klastrów,

2. oblicz odległość każdego elementu od środka klastra,

3. przypisz elementy do tego klastra, do którego odległość są najmniejsza,

4. dla każdego z powstałych klastrów (składających się teraz ze zbioru elementów) oblicz wartość średnią – będzie ona nowym środkiem klastra,

5. powtarzaj kroki 2, 3, 4 do czasu aż kolejne iteracje nie będą powodować żadnych zmian w przynależności elementów do klastrów albo do osiągnięcia maksymalnej liczby iteracji.

Proste? Proces klasyfikacji polega więc na naprzemiennym sprawdzaniu odległości elementów do środków klastrów i na wyznaczaniu nowych środków po przeprowadzonej klasyfikacji.

MATLAB

W MATLABie powyższy algorytm jest zaimplementowany we funkcji kmeans. Jej działanie pokażę na przykładzie dotyczącym automatycznej klasyfikacji pojazdów samochodowych ze względu na sylwetkę (osobowe, ciężarowe, autobusy, itd.). Dane pojazdów pochodzą z systemu pomiarów parametrów ruchu drogowego, który jest zainstalowany na jednej z dróg krajowych w Polsce.  Cechami, które są łatwo mierzalne przez takie systemy, są między innymi odległości między osiami i długość pojazdu. Wykorzystam te cechy do przeprowadzenia klasyfikacji pojazdów z podziałem na dwie klasy/klastry: pojazdy osobowe i małe busy. Zbiór z danymi można pobrać tutaj i zawiera on dane 2000 pojazdów, gdzie kolumny oznaczają kolejno: data i czas pomiaru, klasa pojazdu, długość, odległość pomiędzy osią 1 a 2. Program jest na końcu wpisu.

Zwróćmy uwagę, że jedna z kolumn ‘VehClass’ zawiera wynik automatycznej klasyfikacji pojazdu przez system pomiarowy. Te dane wykorzystamy do weryfikacji poprawności klasyfikacji algorytmem k-Means.

Program znajduje się na końcu tego wpisu i działanie jest skomentowane w jego treści. Na poniższym rysunku widzimy efekt przeprowadzonej klasyfikacji.

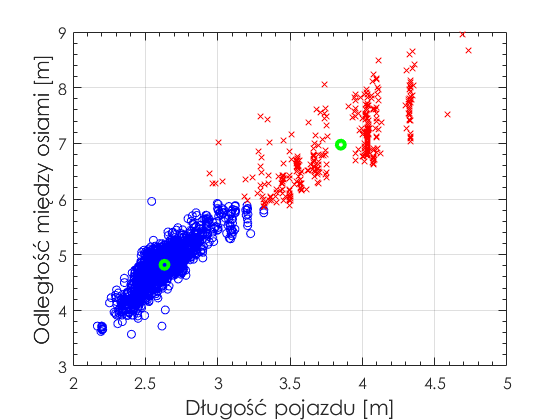
Algorytm wykrył dwa klastry i je zróżnicował. Uzasadnione jest przyjęcie, że wyniki pomiarowe zaznaczone na czerwono należą do klastra pojazdów osobowych (małe rozstawy osi i długość), a na niebiesko do busów (większe wartości cech). Kółkami zaznaczono również środki każdego z klastrów.

Czy ta klasyfikacja jest poprawna? Wykorzystajmy informacje o klasie pojazdu ze zmiennej ‘VehClass’ dostarczonej przez system pomiaru ruchu drogowego i potraktujmy ją jak referencję.

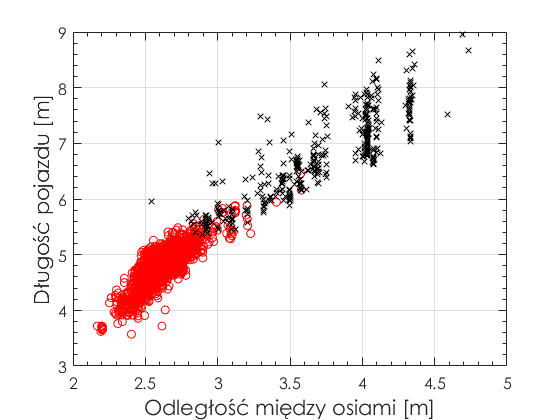
Widać wyraźnie, że klastry w jednym i drugim przypadku są podobne i odpowiadają sobie. A więc algorytm k-means, pomimo braku informacji wstępnej o klastrach, poprawnie je wytypował dzięki zdolności uczenia się! Algorytm ten możecie zastosować praktycznie do dowolnego problemu automatycznej klasyfikacji. Jest tu tylko jedna niepokojąca obserwacja. W danych z systemu elementy w klastrach „nachodzą” na siebie, a granice klastrów są rozmyte. Natomiast po przeprowadzeniu klasyfikacji algorytmem k-means otrzymujemy granice jednoznaczne i ostre. Może więc część pojazdów została źle sklasyfikowana? O tym problemie i innych z zakresu uczenia maszynowego dowiecie się więcej z kolejnego wpisu.

clear all; close all; clc

%% Wczytanie danych i rysunki
load dane_pojazdow

% Rysunek "surowych" danych z podziałem na klasy dokonanym przez 
% system pomiarowy (referencja). VehClass = 1 to pojazdy osobowe, 
% a VehClass = 4 to busy.
figure; scatter(clDataSel.AxleDist1_2(clDataSel.VehClass == 1), clDataSel.Length((clDataSel.VehClass == 1)),'ro')
hold on; 
scatter(clDataSel.AxleDist1_2(clDataSel.VehClass == 4), clDataSel.Length((clDataSel.VehClass == 4)),'kx')
xlabel('Odległość między osiami [m]');
ylabel('Długość pojazdu [m]');
grid on

%% Klasyfikacja (algorytm k-Means)

% Liczba klastrów
noClusters = 2;

% k-Means:
[cindx,ccenter] = kmeans([clDataSel.AxleDist1_2 clDataSel.Length],noClusters,'dist','sqeuclidean');

% Rysunki
figure; 
symbole = {'bo','rx'}; 
for i = 1 : noClusters
    cluster = find(cindx==i);
    plot(clDataSel.AxleDist1_2(cluster),clDataSel.Length(cluster),symbole{i});
    hold on
end
plot(ccenter(:,1),ccenter(:,2),'go','LineWidth',3);
xlabel('Odległość między osiami [m]');
ylabel('Długość pojazdu [m]');
grid on