Jesteśmy przyzwyczajeni do rysowania różnych charakterystyk w skali liniowej. Często jednak można się spotkać z rysunkami, w których oś Y jest wyskalowana w decybelach. Czym są decybele, jak i kiedy je stosować i jak robi się to w MATLABie?
Decybele - interpretacja
Myśląc o decybelach należy pamiętać o jednej bardzo ważnej rzeczy: wyrażają one informacje o stosunku dwóch liczb, z których jedna pełni rolę wartości referencyjnej. Decybele pozwalają więc ocenić o ile jedna wartość jest większa lub mniejsza w stosunku do wartości referencyjnej. Dzięki właściwości funkcji logarytm (o czym później) korzyści ze stosowania decybeli uwidaczniają się jeżeli mamy do czynienia z bardzo dużym zakresem liczb (na przykład od jedności do miliona) oraz wtedy kiedy chcemy rozróżnić niewielkie zmiany wartości na tle całego zakresu zmienności liczb.
Popatrzymy na następujący przykład.
Załóżmy, że dokonujemy pomiaru mocy elektrycznej dla prądu stałego na rezystorze o wartości R. W nominalnych warunkach, czyli dla znamionowych wartości prądu i napięcia, moc ta wynosi 1 W – to będzie nasza wartość referencyjna. Wykonując jednak kolejne pomiary obserwujemy, że mierzona moc rośnie: 2 waty, 10 watów, 100 i dla ostatniego pomiaru wynosi ona 100 tysięcy watów. Policzmy stosunki zmierzonych mocy do mocy nominalnej i narysujmy ich wykres w funkcji liczby kolejnych pomiarów.


Jak widać mamy tu dwa problemy... Po pierwsze występuje bardzo duży zakres zmian mierzonej mocy w stosunku do mocy referencyjnej równej 1 wat. Nieintuicyjnie i trudno jest mówić, że coś jest większe od czegoś innego o trzydzieści pięć tysięcy razy lub pięćdziesiąt tysięcy razy.
Po drugie małe różnice, czy też krotności mocy referencyjnej są nierozróżnialne na wykresie i zwyczajnie nie jesteśmy w stanie odczytać stosunku Pn do P0. Jak ten problem rozwiązać?
Decybele i funkcja logarytm
Stosunek dwóch mocy (i tylko mocy!) wyrażony w decybelach obliczamy według
poniższej zależności. Obliczmy decybele dla naszych pomiarów i narysujmy wykres
w skali decybelowej.


Cóż za zmiana jakościowa! Zastosowanie decybeli spowodowało, że zmieniła się skala. Nie mamy już wartości od 0 do 100 000 ale od 0 do 50. Po drugie nierozróżnialne wcześniej stosunki mocy dla pomiarów 1 – 4 teraz są bardzo wyraźne! Rozwiązaliśmy więc obydwa problemy z rysunku ze skalą liniową (kolor niebieski). Wartości decybeli dla charakterystycznych stosunków mocy zawiera poniższa tabela. Zwróćmy uwagę, że dwukrotny wzrost mocy to 3dB, moc dwa razy mniejsza od referencyjnej to -3dB. Jeżeli moc wzrośnie 10x w stosunku do P0, to w decybelach jest to 10dB, jeżeli moc zmaleje 10x to otrzymujemy -10dB, i tak dalej.
clear all; close all; clc
n = [1 2 3 4 5 6]; % numer pomiaru
y = [2 10 100 1000 10000 100000]; % stosunek mocy
ydB = 10*log10(y);
figure;
plot(n,y,'-o','LineWidth',2)
grid on;
xlabel('Numer pomiaru')
ylabel('P_{n}/P_{0}')
yyaxis right
plot(n,ydB,'-o','LineWidth',2)
grid on;
ylabel('10*log(P_{n}/P_{0})')
Decybele dla innych wielkości niż moc
Z powyższej definicji wynika, że decybele można stosować wyłącznie aby obliczyć stosunek dwóch mocy. Ale wykorzystując cechy funkcji logarytm oraz zależność mocy od kwadratu mierzonej wielkości (np. R*I^2) możemy powyższy wzór przekształcić w taki sposób, aby można było obliczać stosunek na przykład prądu, napięcia i innych wielkości. Wtedy stosujemy następujący wzór:

Przykładem zastosowania decybeli dla napięcia jest wyznaczenie charakterystyki częstotliwościowej danego elementu (filtru, przyrządu pomiarowego czy po prostu widma sygnału).
Przykład - wpływ okna czasowego na widmo badanego sygnału
Załóżmy, że mamy sygnał składający się z trzech sinusów, dla którego wykonujemy analizę widmową, przy czym raz używamy okna prostokątnego, a raz okna Gaussa. Chcemy ocenić, które okno lepiej się sprawdza w sensie rozdzielczości amplitudowej i częstotliwościowej. Jeżeli narysujemy widmo sygnału dla obydwu okien w skali liniowej to trudno jest powiedzieć, które daje lepsze rezultaty.
clear all; close all;
% parametry próbkowania
fpr=1000; dt=1/fpr; % częstotliwość próbkowania (dobrana tak by było spełnione twierdzenie o próbkowaniu)
t0=0.5; % czas obserwacji sygnałów
N=t0/dt; % liczba próbek
t=(0:N-1)*dt; % wektor czasu
df=fpr/N; f=df*(0:N-1); % wektor częstotliwości (potrzebny przy analizie fft)
%% parametry sygnałów
A1=1; f1=50; fi1=0; % amplituda, częstotliwość, przesunięcie fazowe
A2=0.5; f2=125; fi2=pi/2;
A3=0.3; f3=200; fi3=0;
%% generowanie sygnału zawierającego trzy sinusy o f1, f2 i f3
y2 = A1*sin(2*pi*f1*t+fi1) + A2*sin(2*pi*f2*t+fi2) + A3*sin(2*pi*f3*t+fi3);
%% widmo
Y2 = 2 * abs(fft(y2)) / N;
Y21 = 2 * abs(fft(y2.*gausswin(length(y2))')) / N;
%% Rysunki
subplot(423); plot(t,y2); grid on; xlabel('Czas [s]');ylabel('Amplituda'); title(['Sygnał o f1=' num2str(f1) 'Hz, ' 'f2=' num2str(f2) 'Hz, ' 'f3=' num2str(f3) 'Hz']);
figure; plot(f(1,(1:N/2)),Y2(1,(1:N/2)));
hold on; plot(f(1,(1:N/2)),Y21(1,(1:N/2)));
xlabel('Czestotliwość [Hz]')
ylabel('Moduł FFT');
title('Skala liniowa'); grid on;
legend('Okno prostokątne', 'Okno Gaussa')
figure;
plot(f(1,(1:N/2)),20*log10(Y2(1,(1:N/2))));
hold on; plot(f(1,(1:N/2)),20*log10(Y21(1,(1:N/2))));
xlabel('Czestotliwość [Hz]')
ylabel('Moduł FFT');
title('Skala decybelowa'); grid on;
legend('Okno prostokątne', 'Okno Gaussa')

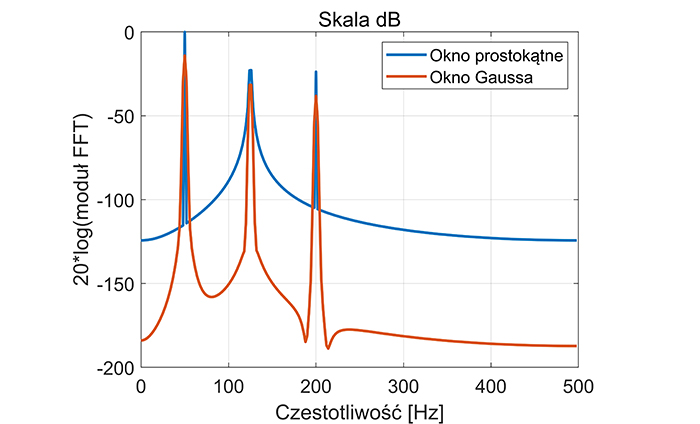
Jeżeli jednak, to samo widmo narysujemy w skali decybelowej, przyjmując za wartość odniesienia maksimum pierwszej sinusoidy, naszym oczom ukaże się zupełnie inny obraz:

Subtelne różnice w charakterystykach częstotliwościowych dla różnych okien widać wyłącznie w skali decybelowej. Widzimy, że dzięki zastosowaniu okna Gaussa otrzymujemy lepszą rozdzielczość amplitudową oraz ograniczenie przecieku widma dla częstotliwości 125Hz. W skali liniowej taka ocena byłaby niemożliwa.
Decybele w MATLABie
Decybele można obliczać według podanych powyżej wzorów lub użyć gotowych funkcji MATLABa. Jest to szczególnie wygodne, gdy chcemy przeliczyć decybele na wartości stosunku mocy czy napięcia. Nie trzeba wtedy „odwracać” wzorów, a wystarczy użyć jednej z poniższych funkcji:
db, db2mag. db2pow, mag2db, pow2db.