Pojęcie różniczkowanie oraz pochodna najczęściej kojarzą nam się z czymś bardzo skomplikowanym i niepotrzebnym. Tymczasem pochodna często gości w świecie nauki i techniki dając nam cenne informacje min. o szybkości zmian danej wielkości fizycznej. Przyglądnijmy się zatem w jaki sposób poprawnie numerycznie obliczyć pochodną w MATLABie.
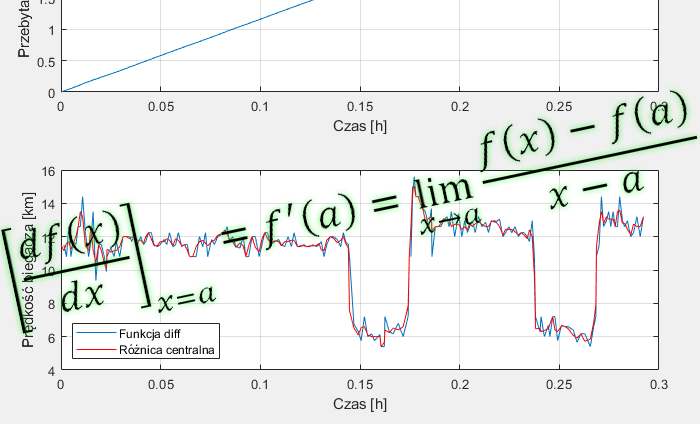
Załóżmy, że dysponujemy danymi pomiarowymi ze smartwatch’a lub zegarka biegowego, które opisują przebytą przez nas drogę. Chcemy poznać prędkość z jaką poruszaliśmy się w trakcie treningu, tak aby móc ocenić jego intensywność. Musimy więc obliczyć szybkość zmian naszego położenia w czasie, czyli prędkość. Z pomocą przychodzi tu pochodna. Na poniższym rysunku, jest przedstawiony wykres położenia i prędkości biegacza w funkcji czasu. Prędkość została obliczona na podstawie przebytej drogi, z zastosowaniem różniczkowania numerycznego. Po lekturze tego artykułu, będziecie wiedzieć jak poprawnie obliczać pochodną w sposób numeryczny w MATLABie, a na końcu znajdziecie przykład skryptu z funkcją obliczającą pochodną. Sam MATLAB nie posiada takiej funkcji.

Zacznijmy jednak od definicji. Pochodna jest miarą szybkości zmian danej wielkości fizycznej i występuje w wielu dziedzinach życia, szczególnie w inżynierii. Definicja pochodnej f’(x) dla funkcji f(x), w punkcie x = a jest następująca:


Przykładem zastosowania pochodnej jest wspomniana relacja jaka występuje pomiędzy przebytą drogą (położeniem), prędkością a przyspieszeniem ciała. Jeżeli położenie ciała wzdłuż osi x jest zdefiniowane jako funkcja czasu x=f(t), to prędkość tego ciała v(t), jest pochodną położenia względem czasu v(t)=dx/dt. Innymi słowy v(t) jest szybkością zmian położenia ciała w danej chwili czasu. Analogicznie, przyspieszenie ciała a(t), jest miarą szybkości zmian prędkości, a więc jest to pochodna prędkości względem czasu a(t)=dv/dt. W fizyce „tempo” przekazywania energii czyli moc jest zdefiniowana przez pochodną. Z kolei w elektrotechnice wartość chwilowa napięcia na cewce jest proporcjonalna do szybkości zmian prądu, czyli pochodnej. Zastosowanie pochodnej jest szerokie i wykracza poza przytoczone przykłady. Wystarczy tu wspomnieć o obliczaniu ekstremów funkcji.
Analityczne obliczanie pochodnej w MATLABie? Tak! Da się to zrobić!
Wielkość poddawana różniczkowaniu może być opisana za pomocą funkcji lub możemy mieć do czynienia ze zbiorem spróbkowanych danych pomiarowych jak w przypadku smartwatch’a. Jeżeli dana wielkość jest opisana za pomocą wyrażenia matematycznego to pochodną można obliczyć w sposób analityczny. Nie zawsze jest to łatwe, a w niektórych przypadkach niemożliwe. Z pomocą przychodzi tu Symbolic Math Toolbox w MATLABie, zawierający zestaw funkcji do obliczeń na wyrażeniach matematycznych w postaci symbolicznej. Efekt działania tego toolboxa można porównać do obliczeń jakie przeprowadzalibyśmy na kartce papieru. Zapisywane formuły, funkcje, równania mają postać symboliczną i w takiej samej postaci otrzymuje się wynik. Do tworzenia zmiennych i funkcji symbolicznych w MATLABie służy funkcja syms, a do obliczania pochodnej funkcja diff. Poniższy przykład ilustruje symboliczne obliczenie pochodnej dla wielomianu 3-go stopnia: x^3 + 2*x^2 + x + 5 (pochodna: 3*x^2 + 4*x + 1):
syms x f = x^3 + 2*x^2 + x + 5 diff(f)
jako wynik otrzymamy:
ans = 3*x^2 + 4*x + 1
I jeszcze dwa inne przykłady dla znanych funkcji.
f1 = log(x) diff(f1) % wynik: ans = 1/x f2 = sin(x) diff(f2) % wynik: ans = cos(x)
Wszystkie wyniki są poprawne. Zastosowanie narzędzi z Symbolic Math Toolbox, jest pomocne jeżeli znamy postać funkcji dla której chcemy obliczać pochodną. A co w sytuacji gdy dysponujemy jedynie danymi pomiarowymi?
Numeryczne obliczanie pochodnej
Jeżeli nie znamy opisu analitycznego funkcji, ale dysponujemy danymi pomiarowymi, to pochodną obliczamy w sposób numeryczny. Można wyróżnić dwie zasadnicze metody numerycznego obliczania pochodnej: metodę różnic skończonych i metodę funkcji aproksymującej. To drugie podejście polega na aproksymacji danych pomiarowych modelem (funkcją), a następnie na analitycznym obliczeniu pochodnej wg sposobu opisanego w poprzednim punkcie. Podejście to jest zalecane, jeżeli w danych występują zakłócenia losowe i znaczny rozrzut wyników pomiarowych. O aproksymacji był jeden z poprzednich wpisów na blogu. Na poniższym rysunku po lewej stronie jest zobrazowane obliczanie pochodnej za pomocą metody różnic skończonych, a po prawej za pomocą funkcji aproksymującej.

Przyglądnijmy się bliżej metodzie różnic skończonych. Polega ona na przybliżeniu pochodnej w punkcie xi, na podstawie wartości z punktów sąsiadujących. Dokładność takiego przybliżenia zależy od wybranej metody różniczkowania, danych pomiarowych (zakłócone lub nie) i okresu próbkowania. Wyróżniamy trzy podstawowe metody różniczkowania:
- różnicę w przód:

- różnicę w tył:

- różnicę centralną:

Przykład: Rozpatrzmy numeryczne obliczanie pochodnej funkcji f(x)=x^3, dla argumentu x=3. Wartość pochodnej tej funkcji wynosi f’(x)=3x^2, a dla argumentu x=3, f’(3)=27. Zobaczmy jaki będzie błąd przybliżenia pochodnej metodami różnic skończonych, dla dwóch wektorów argumentów funkcji:
- x=[2 3 4]; % punkty sąsiaduje odległe o 1
- x=[2.75 3 3.25] % punkty sąsiadujące odległe o 0.25
clear all; close all; clc
% prawdziwa wartość pochodnej
f_prim_pr = 27;
%% Przypadek 1
% wartości argumentów funkcji
x=[2 3 4];
disp('Przypadek 1, dla wartości argumentów x=[2 3 4]')
% różnica w przód
f_prim = (f(x(3)) - f(x(2))) / (x(3) - x(2))
blad = 100 * abs((f_prim - f_prim_pr) / f_prim_pr)
% różnica w tył
f_prim = (f(x(2)) - f(x(1))) / (x(2) - x(1))
blad = 100 * abs((f_prim - f_prim_pr) / f_prim_pr)
% różnica w centralna
f_prim = (f(x(3)) - f(x(1))) / (x(3) - x(1))
blad = 100 * abs((f_prim - f_prim_pr) / f_prim_pr)
%% Przypadek 2
% wartości argumentów funkcji
x=[2.75 3 3.25];
disp('Przypadek 2, dla wartości argumentów x=[2.75 3 3.25]')
% prawdziwa wartość pochodnej
f_prim_pr = 27;
% różnica w przód
f_prim = (f(x(3)) - f(x(2))) / (x(3) - x(2))
blad = 100 * abs((f_prim - f_prim_pr) / f_prim_pr)
% różnica w tył
f_prim = (f(x(2)) - f(x(1))) / (x(2) - x(1))
blad = 100 * abs((f_prim - f_prim_pr) / f_prim_pr)
% różnica w centralna
f_prim = (f(x(3)) - f(x(1))) / (x(3) - x(1))
blad = 100 * abs((f_prim - f_prim_pr) / f_prim_pr)
%% Badana funkcja
function ff = f(x)
ff = x^3;
end
Po uruchomieniu powyższego programu w MATLABie, wyniki pojawią się w command window. Z przedstawionych obliczeń wynikają dwa wnioski. Po pierwsze najdokładniejsza w rozpatrywanym przypadku jest metoda różnicy centralnej. Po drugie im mniejsze zmiany argumentów (w przypadku sygnałów okresu próbkowania) tym przybliżenie pochodnej jest dokładniejsze.
Co z naszym biegaczem?
Na koniec wróćmy do przykładu z początku artykułu. Jak obliczyć pochodną jeżeli dysponujemy spróbkowanymi danymi pomiarowymi? Dane z zegarka biegowego znajdują się tutaj. Możecie je pobrać i sami spróbować obliczyć prędkość biegacza. Jeśli wolicie gotowe rozwiązanie to poniżej znajduje przykładowy program.
Na końcu skryptu jest treść funkcji obliczającej pochodną metodą różnicy centralnej, z uwzględnieniem obliczania pierwszej i ostatniej wartości odpowiednio różnicą w przód i w tył.
%% Obliczanie prędkości biegacza na podstawie jego położenia
% Dane pomiarowe pochodzą z zegarka biegowego
clear all; close all; clc
%% wczytanie danych
load 2019_garmin_data
%% "Proste" obliczanie pochodnej przez funkcje diff (tracimy jedną próbkę)
dx = diff(x);
dt = diff(t);
V = dx./dt;
subplot(211); plot(t,x); xlabel('Czas [h]'); ylabel('Przebyta droga [km]'); grid on;
subplot(212); plot(t(2:end),V); xlabel('Czas [h]'); ylabel('Prędkość biegacza [km]'); grid on;
%% Obliczanie pochodnej metodą różnicy centralnej (funkcja f_prim)
V2 = f_prim(t,x);
hold on; plot(t,V2, 'r')
legend('Funkcja diff','Różnica centralna','Location','southwest')
%% Funkcja obliczająca pochodną metodą różnicy centralnej
function pochodna=f_prim(x,y)
N = length(y);
pochodna = zeros(1,N);
pochodna(1) = (y(2) - y(1)) / (x(2) - x(1));
for i = 2 : N-1
pochodna(i) = (y(i+1) - y(i-1)) / (x(i+1) - x(i-1));
end
pochodna(N) = (y(N) - y(N-1)) / (x(N) - x(N-1));
end
W efekcie działania programu otrzymujemy znany już rysunek:

Dzięki obliczeniu pochodnej położenia po czasie, widzimy jak zmieniała się prędkość biegacza. Można również zaobserwować, że metoda centralnych różnic skończonych daje lepsze (mniej rozrzucone) przybliżenie pochodnej niż bezpośrednie użycie funkcji diff (różnica w przód). Poza tym w przypadku funkcji diff tracimy jedną próbkę.
Artykuł nie wyczerpuje zagadnienia numerycznego obliczania pochodnej. Nie wspomniałem tutaj o szeregach Taylor’a, wielopunktowej metodzie różnic skończonych ani o wielomianach Lagrange’a. Nie poruszyłem również kwestii dokładności przybliżeń. Są to bardziej zaawansowane metody i ich zgłębienie wymaga lektury przedmiotu. Powodzenia w liczeniu pochodnych!